As far as now, CLIMB extends DecSerFlow in two different directions:

• Temporal aspects
• Extended branching formulas

Temporal Aspects

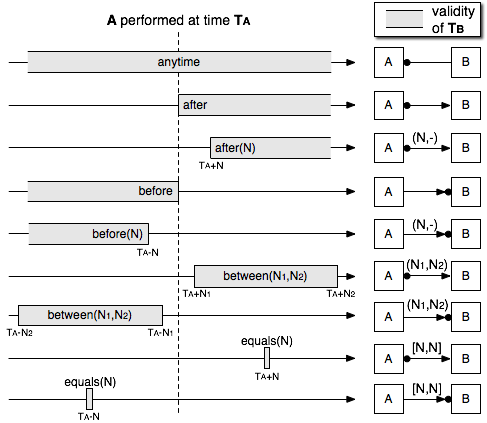
Basic DecSerFlow/Condec constraints do not deal with quantitative temporal aspects, i.e. with the possibility of explicitly reasoning over execution times to express delays and deadlines. Because SCIFF treats execution times as (integer) variables, possibly subject to CLP constraints, CLIMB is seamlessly able to deal with such an issue. For example, to model a constraint such as "After having paid for an item, a receipt must be sent within 2 days" can be simply expressed (supposing that times are expressed in hours) by:

H(performed(payment),Tp)→E(performed(send_receipt),Tr)∧Tr>Tp∧Tr<Tp+48.

DecSerFlow constraints can be therefore extended to represent different temporal aspects, while mantaining a valid underlying semantics in CLIMB (see the following figure).

Extended branching formulas

DecSerFlow supports the possibility of modeling branching constraints, i.e. constraints which involve different target activities. When this is the case, branches are interpreted in a disjunctive manner, i.e. the constraint is satisfied if it is satisfied for at least one target. This resembles the OR split of classical workflow languages; one can therefore ask whether DecSerFlow is able to support other basic split/join constructs of workflow languages. The following table summarizes such constructs, showing that DecSerFlow is able to cover:

• OR split (as described above)
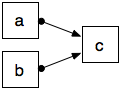
• AND split (indirectly, because the constraint must be explicitly repeated for each target activity)
• OR join (indirectly, because the constraint must be explicitly repeated for each source activity)

What is not supported in DecSerFlow is a synchronization construct, to express that a certain constraint will trigger only when a set of activities has been executed. An example is a syncrhonized response, stating that if two activities have been performed, then another activity must be executed afterwards. Such kind of constraints can be easily represented in CLIMB, because SCIFF rules support a conjunction of happened events in their body.

Type	Representation	Equivalent	Mapping
OR split			H(a,Ta) →E(b,Tb)∧Tb>Ta ∨E(c,Tc)∧Tc>Ta.
AND split			H(a,Ta) →E(b,Tb)∧Tb>Ta. H(a,Ta) →E(c,Tc)∧Tc>Ta.
OR join		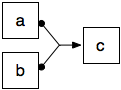	H(a,Ta) →E(c,Tc)∧Tc>Ta. H(b,Tb) →E(c,Tc)∧Tc>Tb.
AND join		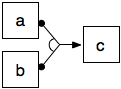	H(a,Ta)∧H(b,Tb) →E(c,Tc)∧Tc>Ta∧Tc>Tb.