Define the improveWithNHood function
 PREVIOUS
NEXT
PREVIOUS
NEXT
| IBM ILOG Dispatcher User's Manual > The Basics > Solving a Vehicle Routing Problem > Solve > Define the improveWithNHood function |
Define the improveWithNHood function |
INDEX
 PREVIOUS
NEXT
PREVIOUS
NEXT
|
After you have found a first solution, you create the neighborhoods you will use in the solution improvement phase. The central idea of the neighborhood is to define a set of solution changes, or deltas, that represent alternative moves that can be taken. Neighborhoods are classified in two groups: those that modify only one route are known as intra-route neighborhoods; those that make changes between routes are known as inter-route neighborhoods. Inter-route neighborhoods can sometimes be used to improve a single route and thus become--strictly speaking--intra-route neighborhoods themselves.
Step 7 - | Create the neighborhoods |
Add the following code after the comment //Create the neighborhoods
void RoutingSolver::improveWithNhood() { IloNHood nhood = IloTwoOpt(_env) + IloOrOpt(_env) + IloRelocate(_env) + IloCross(_env) + IloExchange(_env); _solver.out() << "Improving solution" << endl; |
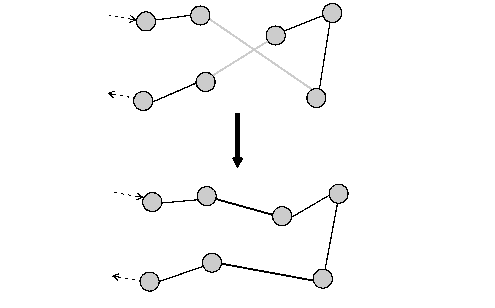
This neighborhood, an instance of IloNHood, is composed of a combination of Dispatcher's predefined neighborhoods. These neighborhoods include: Two-Opt, OrOpt, Relocate, Cross, and Exchange. Figure 3.2 shows how the Two-Opt neighborhood works. In this example, the cost is proportional to the length of the route. The move eliminates the crossing by destroying two arcs and creating two new arcs. The resulting route is shorter, and thus less costly. For information about how the other predefined neighborhoods work, see ïtò^ B Predefined Neighborhoods.
Now, you use iterative improvement techniques to modify the first solution using the neighborhoods you just created. Local search uses search heuristics to guide how the alternative moves in a neighborhood are taken. The search is iterative in that it tries a series of moves in order to decrease the cost of the solution found.
In this lesson, Dispatcher uses the first accept search heuristic. First accept search takes the first legal cost decreasing move encountered. The search continues to take such moves until the neighborhood contains no legal cost-reducing moves. This point is usually termed a local minimum. The word local is used to signify that this point is not guaranteed--and, in fact, is not usually--a global minimum. This method accepts any legal improving move and so is not too expensive in terms of computational cost. Thus, it is preferred when the problem is very large or an optimized solution is required as quickly as possible.
Dispatcher also offers the best accept search heuristic, which works like the first accept except that best accept search takes the legal move from the neighborhood that decreases cost by the greatest amount. Dispatcher also offers metaheuristics, such as guided local search and tabu search, that allow neighborhood moves that degrade the current solution to escape current local minimums. For more information, see ïtò^ C Predefined Search Heuristics and Metaheuristics.
Step 8 - | Improve the solution |
Add the following code after the comment //Improve the solution
IloGoal improve = IloSingleMove(_env, _solution, nhood, IloImprove(_env), _instantiateCost); while (_solver.solve(improve)) { } |
You use the function IloSingleMove to return a goal that makes a single local move as defined by a neighborhood and a search heuristic. The first legal move reducing costs results. The goal scans the neighborhood nhood using _solution as the current solution. The function IloSingleMove will first see if it can make a legal, cost-decreasing move using the neighborhood IloTwoOpt. If it cannot, it tries IloOrOpt, and so on. The search heuristic IloImprove is used to filter moves by implementing a greedy search heuristic. It accepts only new routing plans that strictly decrease the cost and, thus, allows only improvements in the objective. The subgoal _instantiateCost is executed after the deltas from the neighborhood are applied to the current solution.
If a successful move can be found, the goal succeeds. The constrained variables are in the state corresponding to the application of the move. This new state is saved to _solution before the goal succeeds. If no successful move can be found, the goal fails, and _solution is left unchanged. You then use the _restoreSolution goal you created in the RoutingSolver constructor to restore this last solution.
Step 9 - | Restore the last solution |
Add the following code after the comment //Restore the last solution
_solver.solve(_restoreSolution); } |
| © Copyright IBM Corp. 1987, 2009. Legal terms. | PREVIOUS NEXT |