Predefined Search Heuristics and Metaheuristics

Before reading this appendix, you should read the IBM® ILOG® Solver User's Manual chapter on local search. Dispatcher uses Solver's basic local search facilities, while defining its own neighborhoods and metaheuristics.

Basic Search Heuristics

Basic heuristics are those which accept only new routing plans that strictly decrease the cost. For Dispatcher, these comprise two search methods, first accept and best accept. First accept search takes any legal cost decreasing move (the first one encountered), whereas best accept search takes the legal move from the neighborhood that decreases cost by the greatest amount. Both searches continue to take such moves until the neighborhood contains no legal cost-reducing moves. This point is usually termed a local minimum (under the assumption that you are minimizing the objective), as all neighborhood moves are "uphill." The word "local" is used to signify that this point is not guaranteed (and in fact is not usually) a global minimum.

Although the above description entails making improving moves until a local minimum is reached, the local search methods provided by Solver are completely open in the sense that control is returned to user code after each move has been made. Therefore, local search can be stopped at any point along the way should a limit (such as time) be exhausted, or an external event occur requiring the optimization to stop.

First Accept Search

This method accepts any legal improving move and so is not too expensive in terms of computational cost. Thus, it is preferred when the problem is very large or an optimized solution is required as quickly as possible. Dispatcher code to implement a first accept search is shown below. We assume an IloDispatcher (dispatcher), IloRoutingSolution (solution), IloEnv (env), and IloSolver (solver) are already defined.

The following code creates a goal that instantiates the cost to its minimum value (Dispatcher's constraints only provide a lower bound on the cost) and a neighborhood composed of three basic routing neighborhoods (relocate, exchange, and 2-opt).

IloGoal instCost = IloDichotomize(env, dispatcher.getCostVar(), IloFalse);
IloNHood nhood = IloRelocate(env) + IloExchange(env) + IloTwoOpt(env);

A greedy heuristic (which allows only improvements in the objective) called IloImprove is used to reject all degrading moves. The IloSingleMove goal is used to construct a move. As no search selector is passed to it, the first legal move reducing cost results. The instCost goal is executed just before testing each move.

IloMetaHeuristic improve = IloImprove(env);
IloGoal move = IloSingleMove(env, solution, nhood, improve, instCost);

Then a loop is entered, where moves are accepted until no more legal improving ones exist. Finally, the improved solution is moved to Dispatcher's model using the IloRestoreSolution goal.

while (solver.solve(move));
solver.solve(IloRestoreSolution(env, solution));

Best Accept Search

This method accepts the most profitable (in terms of cost) legal improving move and so is more expensive in terms of computational cost than the first accept method just described. For some problems, however, the results can be better than those provided by first accept. You should experiment on your own problem to find the best fit.

In terms of code, performing a best accept search is very much like a first accept search except that a selector is passed to IloSingleMove to select the best neighborhood move. Code for implementing a best accept search is shown below:

IloGoal instCost = IloDichotomize(env, dispatcher.getCostVar(), IloFalse);
IloNHood nhood = IloRelocate(env) + IloExchange(env) + IloTwoOpt(env);
IloMetaHeuristic improve = IloImprove(env);
IloSearchSelector selBest = IloMinimizeVar(env, dispatcher.getCostVar());
IloGoal move = IloSingleMove(env, solution, nhood, improve, selBest, instCost);
while (solver.solve(move));
solver.solve(IloRestoreSolution(env, solution));

MetaHeuristics

The basic search heuristics (which use IloImprove) terminate when no cost-reducing move can be found, at a local minimum. However, in many cases we would like to go on searching, hoping to find better solutions than the one at the current local minimum. To do this, we need to allow neighborhood moves that degrade the current solution to allow the search to move from the current position. However, the ways in which degrading moves are accepted must be carefully controlled to prevent the search from moving to very poor solutions. This more subtle control is provided by what we term metaheuristics.

Dispatcher provides two basic metaheuristics specialized for routing problems. The first of these is a tabu search metaheuristic and the second one is based on guided local search. Various search mechanisms can be created depending upon the way in which these two basic metaheuristics are combined with search selectors. Tabu search and guided local search can also be combined to produce a hybrid, which might be termed guided tabu search.

The following sections detail ways to generate different search methods using the metaheuristics provided with Dispatcher.

Tabu Search Metaheuristic

A detailed description of the operation of Dispatcher's tabu search metaheuristic is given in the IBM ILOG Dispatcher Reference Manual. Here, we give a brief description of its operation.

Objects of the class IloDispatcherTabuSearch allow degrading moves to be accepted by the local search process and attempt to avoid moving the search cycle to places it has previously been. To prevent cycling, a metaheuristic could, of course, store every solution it had visited and forbid a return to any such point. However this has a significant memory burden. Therefore, IloDispatcherTabuSearch uses the popular technique of the tabu list. The tabu list is a list of "features" of a solution that are forbidden, or alternatively, that must be present. Features are added and dropped from a list when a neighborhood move is made.

In Dispatcher, the features are the arcs of the current solution, and two tabu lists are maintained, one that dictates which arcs must not be part of any new solution, and the other that dictates which arcs must be part of any new solution. By maintaining finite lists, tabu search is encouraged to explore solutions with different arcs. The length of time a feature remains on a list (the tenure) is important and affects how driven the search is to avoid solutions which resemble previous ones. This is a parameter of IloDispatcherTabuSearch, and can be altered dynamically during the search process.

Another aspect of IloDispatcherTabuSearch is the aspiration criterion, which allows a neighborhood move to be accepted despite being tabu. The purpose of the aspiration criterion is to prevent the search from being overly inhibited by the tabu process. The aspiration criterion in IloDispatcherTabuSearch makes it possible to accept any move that improves on the best cost found so far.

Guided Local Search Metaheuristic

Guided local search is an alternative to tabu search for allowing the search process to move out of local minima. As in tabu search, how the search can move around is restricted. Guided local search works by making a series of greedy searches, each to a local minimum. However, it reduces a different cost function from the original. If the original cost function is represented by c, then guided local search attempts to reduce the cost c+wp, where p is a penalty term that is adjusted every time a local minimum is reached, and w is a constant. So, in essence, guided local search tries to minimize a combination of the true cost and a penalty term. The weighting constant w is an important search parameter that determines how important the penalty term is with respect to the true cost.

Guided local search is constructed so that the penalty term is higher when the search moves to solutions that resemble previous ones, and in this sense it is similar to tabu search. This is done by recording certain arcs as "bad" each time a local minimum is reached. When these arcs appear in a solution, the penalty term is increased. Guided local search determines which arcs are bad based upon the cost of the arc in the solution and how often that arc has previously appeared at local minima. More complete details of the operation of guided local search are given in the IBM ILOG Dispatcher Reference Manual.

Using Metaheuristics In Search

The tabu search metaheuristic and the guided local search metaheuristic described above are implemented by the classes IloDispatcherTabuSearch and IloDispatcherGLS. IloImprove can be used to create both first and best accept search strategies depending on the choice of search selector used. Similarly, tabu and guided local search can be combined with selectors (and even each other), to produced various types of metaheuristic search strategies for Dispatcher.

Some templates for search strategies using these two metaheuristics are presented in the following sections. You, however, are free to implement more complex strategies. For example, maintaining a set of good solutions found during search, and occasionally restarting search from one of these can be an effective technique.

The following are several variations on a theme for performing search, although since they are largely similar, only the first is presented in detail.

Tabu Search

A basic tabu search process uses the IloDispatcherTabuSearch metaheuristic and takes the best move at each iteration. However, the tabu search metaheuristic is not well suited for taking the first move at each step, as search can move very quickly to poor quality areas of the search space. The following code shows how you might implement a function to perform such a tabu search process. In this code, the tabu tenure is varied during search, which can cut down on the search moving in cycles around the same area.

void RoutingSolver::improveWithTabu() {
  _nhood.reset();
  IloRoutingSolution rsol = _solution.makeClone(_env);
  IloRoutingSolution best = _solution.makeClone(_env);
  IloDispatcherTabuSearch dts(_env, 12);
  IloSearchSelector sel = IloMinimizeVar(_env, _cost);
  IloGoal move = IloSingleMove(_env, rsol, _nhood, dts, sel, _instantiateCost);
  move = move && IloStoreBestSolution(_env, best);
  for (IloInt i = 0; i < 150; i++) {
    if (i == 70) dts.setTenure(20);
    if (i == 85) dts.setTenure(5);
    if (i == 105) dts.setTenure(12);
    if (_solver.solve(move))
      _solver.out() << "Cost = " << _solver.getMax(_cost) << endl;
    else
      if (dts.complete()) break;
  }
  _solver.solve(_restoreSolution);
  rsol.end();
  best.end();
  dts.end();
}

The function resets the neighborhood and set up the various objects used in the search. Resetting Dispatcher's neighborhoods (and indeed metaheuristics) is always recommended before starting a new search, as neighborhoods and metaheuristics maintain internal data structures which are well defined within a single search, but not if search is restarted from an arbitrary point. As you are creating the tabu search metaheuristic, there is no need to reset it, but the neighborhood is passed here, and so a reset is performed.

Two duplicates are made of the current solution--one to be used during search and one to store the best solution found during search. The first is made as you do not wish to change the solution passed, only to present the improved solution on return from the function. The second is made because with search methods that can accept cost degrading moves, the best solution found is not necessarily the current solution.

The tabu search metaheuristic is created with an initial tenure of 12 moves.

The goal to make a single move is constructed using IloSingleMove. Then, a secondary goal (IloStoreBestSolution) is attached that stores the new solution as the best one if its cost is better than the previous best.

The optimization loop is then entered, making up to a maximum of 150 moves, or stopping when no move could be made and the metaheuristic returns IloTrue from its complete method.

The tenure can be dynamically changed during search, and this is demonstrated by changing its value after certain numbers of iterations. Other techniques you can use are to change the tenure to a random value in a range every so many iterations, or to perform such a change after a certain number of iterations without improvement to the best solution found.

Finally, the best solution is restored, and the memory for the temporary solutions reclaimed by using IloSolution::end().

The following figure shows an example of the variation of the cost using such a tabu search on a VRP. The x-axis represents the number of iterations performed.The y-axis represents the value of the cost. The dashed line represents the best cost found so far for a given iteration, while the solid line represents the current cost function. From this figure, you can see the basic descent during the first iterations (when the dashed line is overlapped by the solid line), then degrading moves are used to explore the search space and eventually improve the best solution.

Guided Local Search

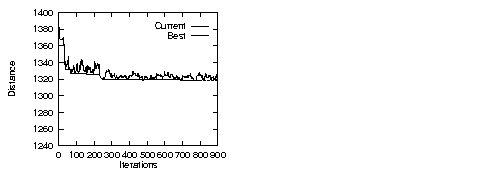
There are two basic types of search that can be performed using the guided local search (GLS) metaheuristic, depending upon which type of search selector is used to choose the neighborhood move. You can choose the best legal move at each stage, resulting in the code shown below:

void RoutingSolver::improveWithGLS() {
  _nhood.reset();
  IloRoutingSolution rsol = _solution.makeClone(_env);
  IloRoutingSolution best = _solution.makeClone(_env);
  IloDispatcherGLS dgls(_env, 0.2);
  IloSearchSelector sel = IloMinimizeVar(_env, dgls.getPenalizedCostVar());
  IloGoal move = IloSingleMove(_env, rsol, _nhood, dgls, sel, 
_instantiateCost);
  move = move && IloStoreBestSolution(_env, best);
  IloCouple(_nhood, dgls);
  for (IloInt i = 0; i < 150; i++) {
    if (_solver.solve(move))
      _solver.out() << "Cost = " << _solver.getMax(_cost) << endl;
    else {
      _solver.out() << "---" << endl;
      if (dgls.complete()) break;
    }
  }
  IloDecouple(_nhood, dgls);
  IloGoal restoreSolution = IloRestoreSolution(_env, best) && _instantiateCost;
  _solver.solve(restoreSolution);
  rsol.end();
  best.end();
  dgls.end();
}

There are two peculiarities which are markedly different from the previous tabu search example. The first are the lines of code using IloCouple and IloDecouple. These functions connect (and disconnect) a neighborhood to a metaheuristic. The neighborhood must be coupled to an instance of IloDispatcherGLS otherwise an IloException is thrown when you try to use the instance in the search.

The following figure shows the variation of the cost using GLS on the same VRP as the Tabu Search example. The x-axis represents the number of iterations performed. The y-axis represents the value of the cost. The dashed line represents the best cost found so far for a given iteration, while the solid line represents the current cost function. From this figure, you can see the basic descent during the first iterations (when the dashed line is overlapped by the solid line), then degrading moves being used to explore the search space and eventually improve the best solution. What can be seen from this figure is that the "jumps" of the GLS metaheuristic are much larger than those of the basic Tabu Search. This is the consequence of the long-term memory feature of GLS. On this example also, GLS gives better results than Tabu Search.

Guided Tabu Search

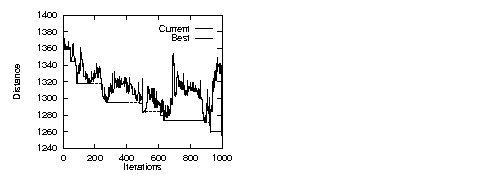
Simple Tabu Search and Guided Local Search can be mixed together. Arcs present in the solution are penalized just as with GLS, while a tabu list is handled just as in tabu search. Therefore, the short-term memory feature of simple tabu search is enhanced with a long-term memory, acting as a diversifying scheme.This results in a very effective metaheuristic, that can often produce good quality solutions in much fewer iterations than either simple Guided Local Search or Tabu Search.