Predefined Neighborhoods
 PREVIOUS
NEXT
PREVIOUS
NEXT
| IBM ILOG Dispatcher User's Manual > Developing Dispatcher Applications > Predefined Neighborhoods |
Predefined Neighborhoods |
INDEX
 PREVIOUS
NEXT
PREVIOUS
NEXT
|
Dispatcher offers a variety of predefined neighborhoods for use in improving a solution. Each predefined neighborhood is explained in this appendix.
The heuristics that generate a first solution to a routing problem find a "good" feasible solution very quickly. These first solutions can be further improved by using neighborhoods to reduce the costs of the routes they find. The central idea of the neighborhood is to define a set of solution changes, or deltas, that represent alternative moves that can be taken. Neighborhoods are classified in three groups: those that modify only one route are known as intra-route neighborhoods; those that make changes between routes are known as inter-route neighborhoods; and those that change whether visits are performed or not. Interestingly enough, the inter-route neighborhoods can sometimes be used to improve a single route and thus become intra-route neighborhoods themselves.
The following predefined neighborhoods are provided by Dispatcher: Two-Opt, Or-Opt, Relocate, Cross, Exchange, and several neighborhoods that change whether visits are performed or not.
| Note |
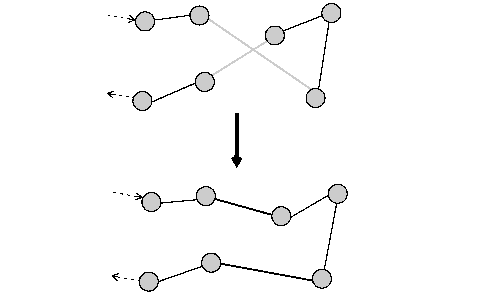
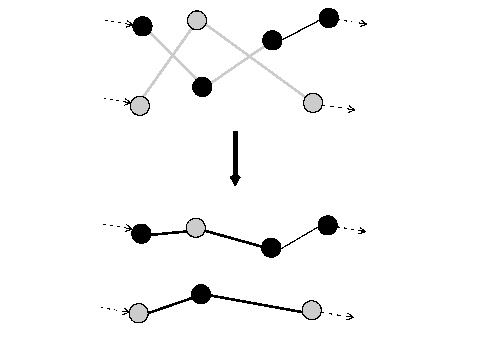
In a Two-Opt neighborhood two arcs in a single route are cut and reconnected to improve the total cost of the route, as follows:
With this neighborhood, directional flows between visits may be reversed. The presence of tight time constraints can therefore decrease its effectiveness. Two-Opt is implemented by the function IloTwoOpt.
The following figure illustrates this process. Here, we assume that the cost is proportional to the length of the route. The move eliminates the crossing by destroying two arcs and creating two new arcs. The resulting route is shorter, and thus less costly.
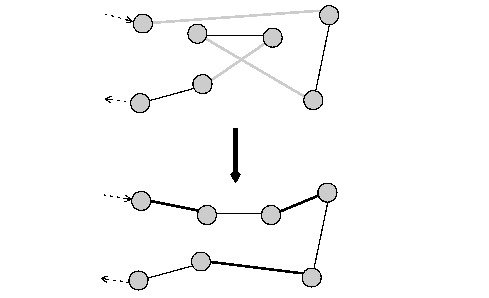
In an Or-Opt neighborhood segments of visits in the same route are relocated.
Or-Opt is implemented by the function IloOrOpt.
The following figure illustrates the process. Here, the cost is assumed to be proportional to the length of the route. The move eliminates the crossing by destroying three arcs and creating three new arcs. The resulting route is shorter, and thus less costly.
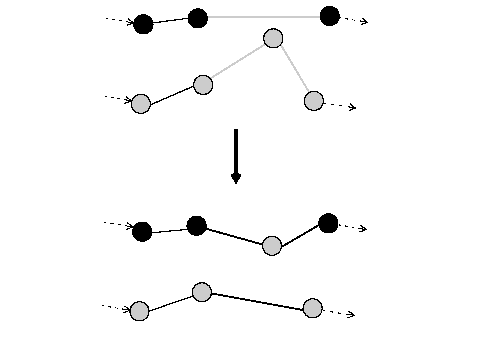
In a relocate neighborhood a visit is inserted in another route if all constraints--such as capacity and time--are still satisfied. This method can be generalized if more than one visit of a route is moved at the same time. When pairs of visits are moved, the neighborhood is useful for optimizing problems such as the Pickup-and-Delivery Problem (PDP). Relocate is implemented by the function IloRelocate.
The following figure shows the process. Here, we assume that the cost is proportional to the length of the route. The move destroys three arcs and creates three new arcs. As a result total travel distance, and thus cost, is less.
The function IloFPRelocate returns a neighborhood that modifies a solution by relocating individual visits to a new position in another route. This function is similar to IloRelocate for PDP problems, except that it explores more options for the delivery component of a pickup- delivery pair that is being relocated. For example, consider two pairs of pickup-delivery visits: p1-d1 and p2-d2. IloRelocate would try to move p2 after p1 and d2 immediately after d1. IloFPRelocate would try to move p2 after p1, and then try to locate d2 at every position after d1. Thus, this neighborhood is potentially larger than that created by IloRelocate.
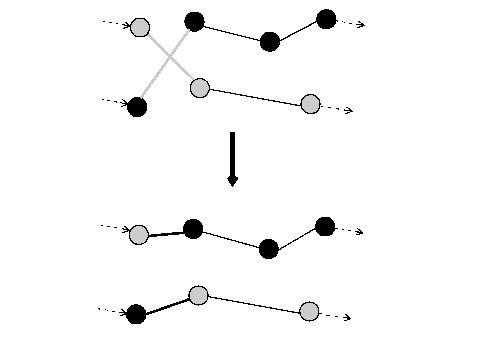
In a cross neighborhood the ends of two routes are exchanged: the first part of route A is connected to the last part (end) of route B and the first part of route B is connected to the last part (end) of route A. Cross is implemented by the function IloCross.
The following figure illustrates the process. The cost is assumed to be proportional to the length of the route. The move eliminates the crossing by destroying two arcs and creating two new arcs. The resulting routes are shorter, and thus less costly.
In an exchange neighborhood, two visits of two different routes swap places if all constraints are still satisfied. This method can be generalized if more than one visit of a route is exchanged at the same time. When a pair of visits is exchanged, this neighborhood is useful for optimizing problems such as the Pickup-and-Delivery Problem (PDP). Exchange is implemented by the function IloExchange.
The following figure shows the process. The cost is assumed to be proportional to the length of the route. The move eliminates the crossings by destroying four arcs and creating four new arcs. The resulting routes are shorter, and thus less costly.
Dispatcher provides predefined neighborhoods that change whether a visit is performed or not.
The function IloMakePerformed returns a neighborhood that modifies a solution by inserting an unperformed visit after a performed one. The function IloMakePerformedPair returns a neighborhood that modifies a solution by making an unperformed visit pair performed. For each vehicle route in which the pair is inserted, every combination of positions for the two visits will be tried. This behavior is different from the one of IloMakePerformed which will only try to move the pair immediately after a performed pair of visits.
The function IloMakeUnperformed returns a neighborhood that modifies a solution by causing a performed visit to be unperformed.
The function IloSwapPerform returns a neighborhood that modifies a solution by exchanging a performed visit with an unperformed one.
| © Copyright IBM Corp. 1987, 2009. Legal terms. | PREVIOUS NEXT |