Predefined First Solution Heuristics
 PREVIOUS
NEXT
PREVIOUS
NEXT
| IBM ILOG Dispatcher User's Manual > Developing Dispatcher Applications > Predefined First Solution Heuristics |
Predefined First Solution Heuristics |
INDEX
 PREVIOUS
NEXT
PREVIOUS
NEXT
|
Dispatcher offers a variety of predefined first solution heuristics for use in generating a first solution. Each predefined first solution heuristic is explained in this appendix. To show how the different predefined first solution heuristics work, their results on the same example problem are shown in each section of this appendix. The following predefined first solution heuristics are provided by Dispatcher: enumeration, savings, sweep, nearest-to-depot, nearest addition, and insertion.
The following example data is used in this appendix to demonstrate how each predefined first solution heuristic works. The goal of the example is to compute a route that starts and ends at the depot and visits each node exactly once. The length of the route is computed according to Euclidean distance.
In the following figure, the depot is represented as a black circle. The other circles represent visits to make at various locations. The coordinates of the depot are (30,40). The capacity of the truck is 50 and there are 11 visits to perform. The tuples (x,y,quantity) of the visits are (17,63,19), (31,62,23), (52,64,16), (21,47,15), (37,52,7), (49,49,30), (42,41,19), (20,26,9), (40,30,21), (52,33,11) and (51,21,5).

Dispatcher provides a basic, complete enumeration method for generating a first solution. The enumeration heuristic builds a solution to the problem using an algorithm that completely explores the search space using backtracking. This method should only be used for small problems.
This heuristic is implemented in Dispatcher as the goal IloDispatcherGenerate.
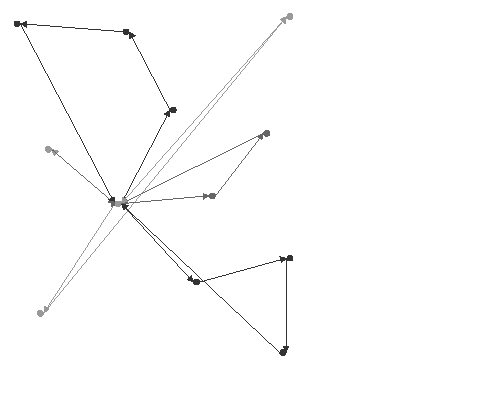
The following figure provides an example of the use of IloDispatcherGenerate on the example VRP with capacity constraints. The cost of this solution is 352.57.
For problems with multiple vehicles, it is very important to consider the trade-off between more vehicles with shorter routes and fewer vehicles with longer routes. For example, the following figure shows two ways of making visits a and b.
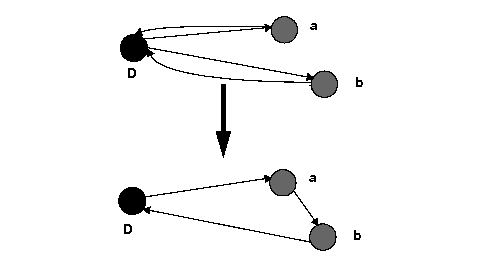
The savings of serving a and b in the same route, denoted savings (a, b), is defined as savings (a, b) = cost (a, Depot) + cost (Depot, b) - cost (a, b). The savings heuristic generates a solution based on this equation. It works like this:
This heuristic is implemented in Dispatcher as the goal IloSavingsGenerate.
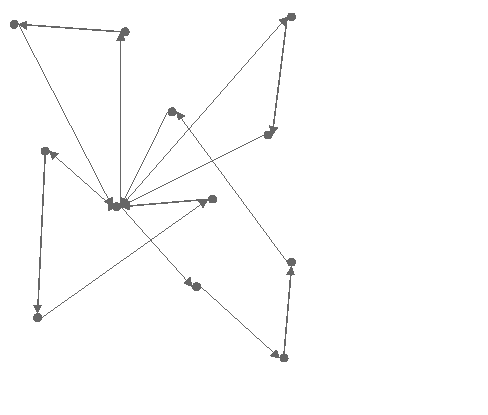
The following figure provides an example of the use of IloSavingsGenerate on the example VRP with capacity constraints. The cost of this solution is 280.947.
The sweep heuristic builds routes by sweeping around the depot:
This heuristic is implemented in Dispatcher as the goal IloSweepGenerate.
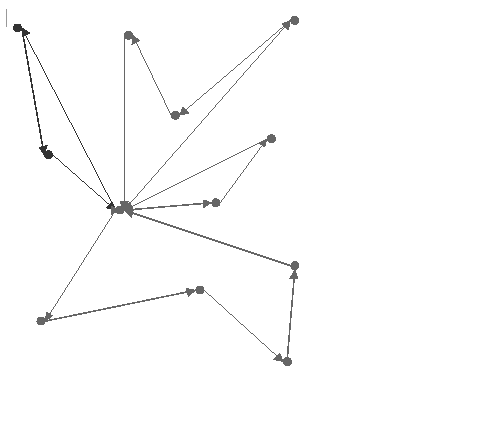
The following figure provides an example of the use of IloSweepGenerate on the example VRP with capacity constraints. The cost of this solution is 270.403.
The nearest-to-depot heuristic builds routes by adding the visits close to the depot first.
For all vehicles:
This heuristic is implemented as the goal IloNearestDepotGenerate.
The following figure provides an example of the use of IloNearestDepotGenerate on the example VRP with capacity constraints. The cost of this solution is 369.297.
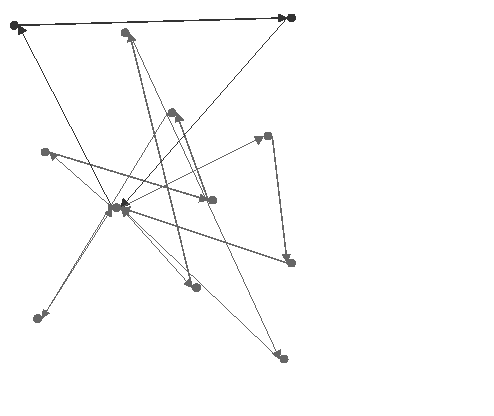
The nearest addition heuristic is very similar to the nearest-to-depot heuristic just described. It often gives better results because the visit added to the route is the one closer to the end of the route, not the one closer to the depot.
For all vehicles:
This heuristic is implemented in Dispatcher as the goal IloNearestAdditionGenerate.
The following figure provides an example of the use of IloNearestAdditionGenerate on the example VRP with capacity constraints.The cost of this solution is 285.232.
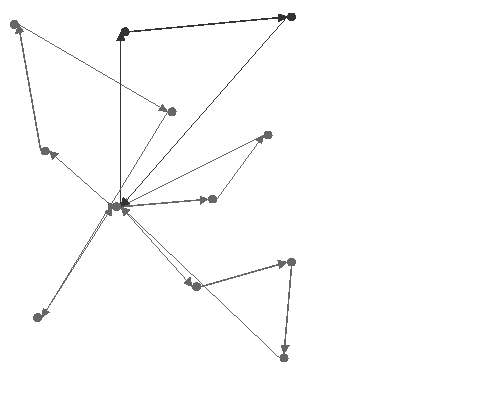
The insertion heuristic works by inserting each visit (in the order they were created) at the best possible place, in terms of cost.
This heuristic is implemented in Dispatcher as the goal IloInsertionGenerate.
The following figure provides an example of the use of IloInsertionGenerate on the example VRP with capacity constraints.The cost of this solution is 300.681.
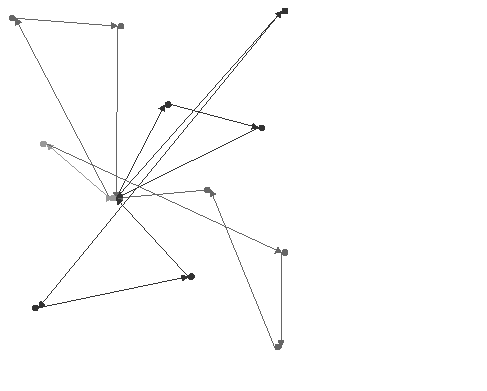
| © Copyright IBM Corp. 1987, 2009. Legal terms. | PREVIOUS NEXT |