| Description |
| Productivity |
| Cost function |
| General case |
| Rounding Policy for Integral Constraints |
Integral and functional constraints address the need for modeling complex dependencies between scheduling variables. Such dependencies makes the use of functions mandatory in order to accurately describe the fine relationships. These constraints concern all the activities processed by a resource. Here are some examples.
A resource often needs to be considered to be unavailable (undergoing maintenance, for instance), which thereby changes the production of an activity as a function of its start time. Consider for example a manufacturing machine which produces half of its capability on Saturday and nothing on Sunday. If the usual capability is 6 pieces per hour, the machine will only produce 3 pieces per hour on Saturday and nothing on Sunday. Stated differently, we need to describe the resource as being 50% productive on Saturday, 0% on Sunday, and 100% for the rest of the week.
With Scheduler, you can model this behavior with the following code.
IloEnv env;
IloModel model(env);
IloGranularFunction week(env, 0, 7, 100);
week.setValue(5, 6, 50);
week.setValue(6, 7, 0);
IloReservoir res(env);
IloActivity act(env, 5);
Model.add(act.produces(res, IloNumVar(env, 1, 10, IloInt)));
IloConstraint productivity = IloResourceIntegralConstraint
(res, IloCapacityVariable, week);
model.add(productivity);
A common use of functional relationships is for making a cost variable dependent on the duration or the end time of an activity.
For instance, the duration of an activity might trigger two different behaviors according to whether it lasts too long or not. Consider an activity that costs 10 units if it is executed fast enough (duration less than 5), but costs only 5 such units if there is enough room for a slow, cheaper, processing.
The cost function would be:
IloGranularFunction costFunction(env, 0, 10); costFunction.setValue(0, 5, 10); costFunction.setValue(5, 10, 5);
A resource taking the profile into account reads:
IloUnaryResource res(env);
IloConstraint cost = IloResourceFunctionalConstraint(res,
IloExternalVariable,
costFunction,
IloDurationVariable);
This constraint states that every activity executing on
res
will have a relation between its duration variable and its external variable. That relation is precisely that specified by
costFunction.
Then we can set an activity's external variable to a given cost variable:
IloNumVar costVariable(env, 0, 10, IloInt); IloActivity act(env, IloNumVar(env, 0, 10, ILOINT)); act.setExternalVariable(costVariable);
and subsequently use this cost in the model.
Scheduler provides modeling tools for two types of relationships: functional and integral constraints.
start
to
end).Data regarding the description of the constraints are stored in an instance of IloGranularFunction. This object primarily consists of a step-wise integer-to-integer function
func, plus an additional parameter, the granularity g.
Given this data, constraints enforcing
Variable1 == f(Variable2)
and

can be added to the model using:
IloConstraint IloResourceFunctionalConstraint(const IloResource resource,
IloSchedVariable leftVar,
const IloGranularFunction curve,
IloSchedVariable rightVar =
IlcDurationVariable) const;
IloConstraint IloResourceIntegralConstraint(const IloResource resource,
IloSchedVariable leftVar,
const IloGranularFunction curve);
Note that the leftVar could be the processing time variable, but in such a
case one has to be sure to not use a calendar object on the corresponding
resource in order to avoid an over-constraint of the problem
(see
Calendars
and IloResource::ignoreCalendarConstraints).
In Scheduler Engine, the following member functions are available:
IlcConstraint IlcResource::makeFunctionalConstraint
(IlcSchedVariable leftVar,
const IlcGranularFunction func,
IlcSchedVariable rightVar =
IlcDurationVariable) const;
IlcConstraint IlcResource::makeIntegralConstraint(IlcSchedVariable leftVar,
const IlcGranularFunction func) const;
The following global functions are available:
IlcIntExp IlcFunctionalExp(const IlcGranularFunction func,
const IlcIntVar x);
IlcIntExp IlcActivityIntegralExp(IlcActivity act,
IlcGranularFunction func);
There are several choices for the variable to be used on the left-side of these constraints, as well as the right-side variable of the functional constraint. These variables are designated by the IloSchedVariable
enumeration in Scheduler Concert Technology and by the corresponding IlcSchedVariable
enumeration in the Scheduler Engine.
When you post a constraint on a resource you enforce that for each resource constraint contributing to the resource, y = = f(x) where x and y are defined with the binding policy (the enumeration). The constraint posted by the user is add(y==IlcFunctionalExp(func,x)), where x and y are Solver variables.
When computing the integral of the function between the start and the end of an activity, the result is usually not a multiple of the granularity
g. As the result of the division by g
must be an integral, rounding occurs. The default rounding mode considers that any raw value of the integral:
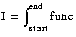
in the range
[x*g, x*g+g)
gives an efficiency equal to
x
after being divided by
g. That means that only the nearest lower integer is taken into account.
For example, let's take a granularity of 100, and a constant function of value 30. Suppose we want to enforce a processing time of 10 with such an integral constraint. The rounding will lead to several possible durations for the activity: d={34, 35, 36}. Indeed, with these three values for the duration, the integral of the function takes the valid values I={1020, 1050, 1080}, all contained in the required range [10*100, 10*100+100).
Several rounding modes can be associated to an instance of a granular function. The rounding mode will be taken into account when creating integral constraints. The enumerations IloGranularFunctionRoundingMode
and IlcGranularFunctionRoundingMode
are available, along with the member functions IlcGranularFunction::setRoundingMode
and IloGranularFunction::setRoundingMode, to change the rounding mode.
Let
func
be a granular function with granularity
g
used within an integral constraint and
x
be a variable ranging in
[xmin, xmax].
Then, the raw integral value:
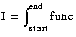
is considered to satisfy the integral constraint
x == I/g
according to the following rounding modes:
IloGranularFunctionRoundUpward: I
is in the range
[xmin*g, (xmax+1)*g).IloGranularFunctionRoundDownward:
I is in the range
((xmin-1)*g, xmax*g].IloGranularFunctionRoundOutward: I
is in the range ((xmin-1)*g, (xmax+1)*g).IloGranularFunctionRoundInward:
I is in the range
[xmin*g, xmax*g].The default rounding mode is IloGranularFunctionRoundUpward.
See Also
IloGranularFunction, IloSchedVariable, IloResource, IloActivity, IloResourceIntegralConstraint, IloResourceFunctionalConstraint, IlcGranularFunction, IlcSchedVariable, IlcResource, IlcGranularFunctionRoundingMode, IloGranularFunctionRoundingMode.