By default an activity is defined by three decision variables: start time (S), end time (E) and duration (D=E-S). In order to accurately model more complex dependencies between activities and their required resources, a fourth decision variable is defined: the processing time (PT), which corresponds to the amount of work the activity performs. The calendar object defines how those variables will interact.

A calendar object is composed by three complementary components:

• A list of shift objects. A shift defines forbidden dates for the start, the end or the wall activity (for example, the activity cannot start during weekends).
• A list of breaks intervals. A break interval defines when the activity is suspended (for example, if breaks are defined by weekends, then an activity with a duration of four days starting on Friday finishes at the end of Wednesday).
• An efficiency curve. The efficiency curve defines the behavior of the duration regarding the start time of activity (for example, if the resource only works at 50% during weekends, then an activity with a nominal duration of four days starting on Friday finishes at the end of Tuesday).

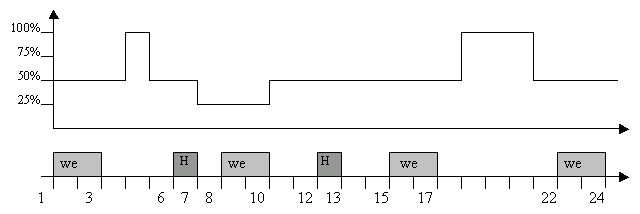
Consider a resource R that is suspended every weekend and during holidays. In addition, R needs to be prepared the day before and the day after each suspension. This preparation will induce a 50% unavailability of R. Such a behavior can be modeled with a calendar constraint defined by an efficiency curve and break intervals as follows:

• An efficiency curve defined between 25% availability (when only one day of work) and 100%;
• A break interval for each weekend and each holiday.

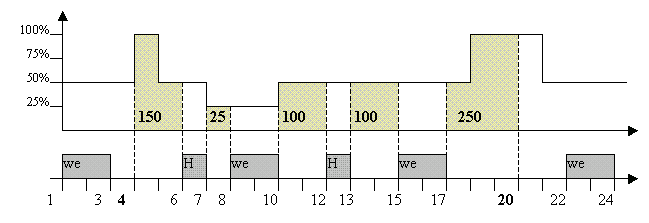
In this example, the processing time of the activity A which starts in S=4 and ends in E=20 is then PT=150+25+100+100+250 = 625% and obviously its duration is D=20-4=16.

If the resource R needs to be switched off before weekends, then weekend break intervals can advantageously be replaced by shift intervals to model this disjunctive behavior. In this case, an activity has to be performed completely inside a week, so an activity with a processing time equal to 2 will be executed at least after time 17.

By default an activity A is defined by three decision variables: start time (S), end time (E), and duration (D=E-S). A fourth variable, called processing Time (PT), is linked to the activity when using a calendar object. This processing time corresponds to the duration of the activity when neither break intervals nor efficiency need to be considered. This can also be called the nominal duration. The relation between start, end and processing time is defined by:

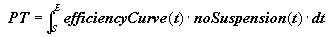
with

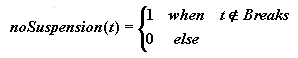
If there are no break intervals and no efficiency curve (by default equal to one on the horizon), PT=E-S=D. In addition to this relationship, activity variables can be overconstrained in the two following ways.

The activity is not breakable corresponds to:

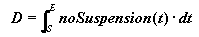
The activity does not use efficiency corresponds to:

A calendar object is defined by a list of shift objects, a list of break intervals, and an efficiency curve. By default, lists are empty and the efficiency curve is equal to 1 on the scheduled horizon. The calendar object is associated with a resource or a resource constraint. When a calendar is defined both on a resource constraint and on the corresponding resource, the calendar of the resource is forgiven in order to only take into account the calendar of the resource constraint.

Consider the example with an activity A, a calendar object C1 associated with the resource R, and a calendar object C2 associated with the resource constraint: A.requires(R). C1 is defined by start shift objects S1 and S2. C2 is defined by break interval B1. Then variables of activity A are constrained by the calendar object C2, and so the start of the activity does not have to respect S1 neither S2.

Activities with null processing time are not affected by calendars. This feature provides an easy way to state that some activities must be "ignored" as far as calendars are concerned.

Consider a breakable activity act that uses efficiency, with a processingTime equal to 4 and two unary resources res1 and res2. There are two calendars C1 (the one of the previous example) and C2 (just a break in [14,19)) and two resource constraints rct1=act.requires(res1) with calendar C1 and rct2=act.requires(res2) with calendar C2. As there is only one activity, there exists only one processingTime variable, and so the processingTime must be equal on both resource constraints (that is, with C1 and C2). As the efficiency is most of the time smaller than 100%, the activity has to be suspended by the break of C2 to be able to respect processingTime==4, as shown on the following figure. The only solution is to start at time 11 and to end at time 20.

So to avoid trouble and express that such an activity requires resource res1 and that the "same" activity also requires resource res2, you must create another activity from the start until the end as defined by resource res1 with the same start and end variables, and a new processing time variable (see IloActivity::shareStartWithStart and IloActivity::shareEndWithEnd).

A shift object is a set of forbidden dates:

An associated type defines the shift behavior regarding the start and the end of the activity. The three types are as follows.

• OnStart: the activity cannot start in the shift, that is:
• OnEnd: the activity cannot end in the shift, that is:
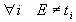
• OnOverlap: the activity cannot overlap a forbidden date, that is:

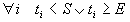
The shift object can be defined by the user using the MACROILOUSERSHIFTOBJECT. However the predefined shift object IloShiftListObject may be enough in most of the cases as it deals with a list of shift intervals.

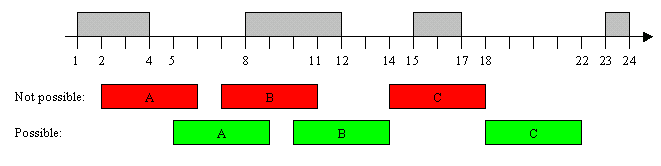
Consider the example with a given the calendar C associated with the resource R, and activities A, B and C all with durations of 4 and requiring R. C is defined by the shift interval list L=[1, 4), [8,12), [15, 17), [23, 24).

• If shift object is OnStart: A cannot start in 2, but it could start in 5;
• If shift object is OnEnd: B cannot end in 11, but it could end in 14;
• If shift object is OnOverlap: C cannot start in 14 and end in 18 because of the shift interval [15,17), but it could start in 18 and end in 22.

Using breaks is the easiest way to model the suspension of an activity by a fixed time interval; so a suspended activity is divided in a set of convex time intervals:

For example:

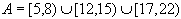
Each time interval I is associated with a unique number called its type (see IloIntervalList in the extensions section of the IBM ILOG Concert Technology Reference Manual. Those types allow one to parameterize the behavior of activities with respect to certain breaks, to ignore breaks, or to express disjunctive behavior. See Disjunctive Break.

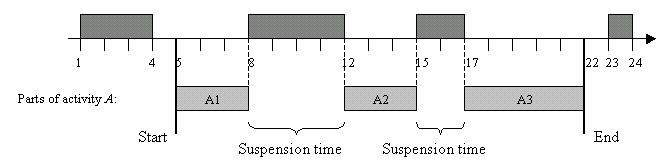
Each activity may be associated with a set of ignored break types. It means that every break B whose type belongs to this set will be ignored, as it does not exist. In the following figure, the activity A with ignored type set {2} is not suspended by breaks 2 whereas the activity B with ignored type set {1} is suspended by breaks 2.

For more information, see IloActivity::addIgnoredBreakType and IloActivity::removeIgnoredBreakType.

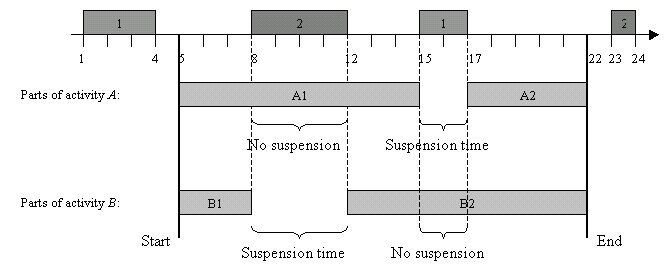
If an activity cannot be suspended at start, then there is no suspension time interval that starts at the start time of the activity.

In the same way, if an activity cannot be suspended at end, then there is no suspension time interval that finishes at the completion time of the activity.

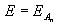
For more information, see IloActivity::setCanBeSuspendedAtStart, IloActivity::setCanBeSuspendedAtEnd, IloActivity::canBeSuspendedAtStart, IloActivity::canBeSuspendedAtEnd.

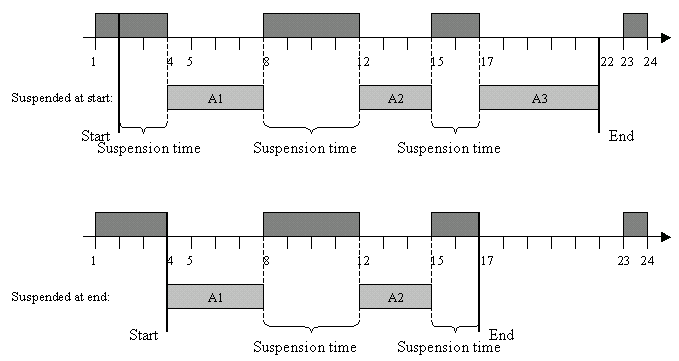
An activity can express the fact that the duration of each of its time intervals must be greater than a threshold duration ExecD.

On the preceding example, the minimal processing duration is 3 (the second processing interval). Thus, if the threshold minimal duration for processing intervals of this activity had been set to 4, the distribution of processing duration depicted in that figure could not be accepted in a solution. See IloActivity::setExecutionDurationMin.

The transition time on a resource allows specifying a delay between two activities (see Transition Times). This delay can take into account the breaks defined on that resource. By default, the transition time on a resource is not suspended by the breaks. This can be illustrated by the following example: suppose a unary resource with a break list [0,2), [7,9), [14,16), and two activities A and B that require this resource. Activity A finishes at time endA=6 and activity B is constrained to start after the end of activity A. If the transition time between A and B is ttAB=10, because of this transition time, the activity B cannot start before date endA + ttAB =16.

The member function void IloTransitionTime::setSuspended(IloBool suspended=IloTrue) allows specifying a transition time that is suspended by the breaks of the resource. In the example above, that would imply that activity B must start after date 20, as shown in the following figure.

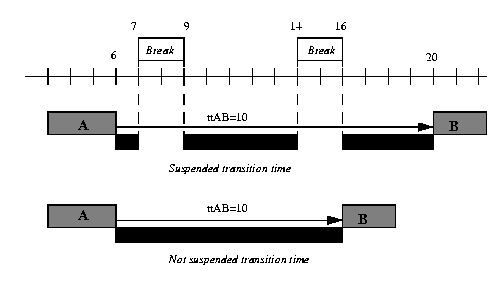
Notice that the transition time on a resource with suspended time concerns all (but only) the breaks on that resource. That is, no calendar object must be defined on resource constraints attached to the resource.

A break B is said to be disjunctive for an activity act if act behaves as a non-breakable activity with respect to this break B. That is, the activity act cannot be suspended by the break.

There are three different ways to implement disjunctive behavior with a calendar:

• Shift object typed as OnOverlap (see Shift Object Semantic). Notice that in most of the cases, using shifts is more efficient than breaks regarding disjunctive behavior.
• Disjunctive break type: Each activity may be associated with a set of disjunctive break types. It means that every break B whose type belongs to this set will be considered as disjunctive for the activity.
• Break size: Each activity may be associated with an interval [dmin, dmax] of possible duration for non-disjunctive breaks. Each break whose duration is outside this interval will be considered as disjunctive for the activity.

A break that is not disjunctive is called a normal break. By default, all the breaks except for null duration breaks are considered as normal (non-disjunctive) breaks for an activity.

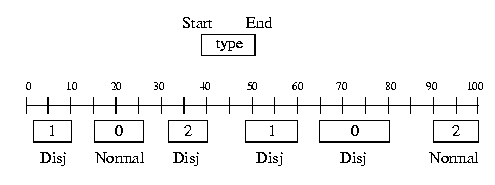
Suppose the break list described in the next figure and an activity whose set of disjunctive break types is 1 and interval of possible duration for normal breaks is [10,12]. The disjunctive status of breaks with respect to this activity is also given on the following figure. For instance, we see that the first break [2,10) will be considered as disjunctive for the activity as its type is 1. The break [15,26) will not be considered as disjunctive because its type does not belong to the set of disjunctive types and its duration (11) falls into the possible durations of normal breaks. The break [32,40) will be considered as disjunctive because its duration (8) does not fall into the possible durations of normal breaks.

For more information, see IloActivity::addDisjunctiveBreakType, IloActivity::removeDisjunctiveBreakType, IloActivity::setDurationMaxNormalBreaks, and IloActivity::setDurationMinNormalBreaks.

The standard use of a break is to suspend the processing time of an activity. In some cases, however, you may want to relax this and allow some limited amount of processing to occur within a break. For example, you might want to specify that it is possible for the end of an activity to be processed inside a break, providing the length of processing time within a break is less than some value. In a factory with one 8-hour shift, where non-shift hours are represented as breaks, it might be better to finish a job as much as a half-hour after the end of the shift rather than to process the entire activity in the next shift.

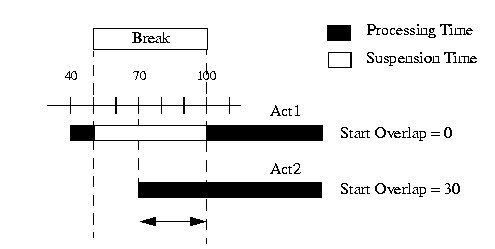
Conceptually, a processing time overlap is a period of time during which the processing time of an activity overlaps a break. Two kinds of processing time overlaps are distinguished:

• Start Overlap
• End Overlap

No other way of overlapping breaks with processing time is allowed.

If an activity act starts (resp. ends) processing in a break B, the duration of the execution overlap between the activity act and break B is called the start overlap (resp. end overlap) of the activity. If the activity does not start in a break, its start overlap is 0. The following figure illustrates two situations together with the value of the start overlap.

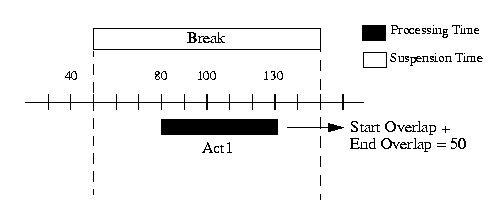
In the special case where the activity starts and ends in the same break, no commitment is made to decide whether the overlap belongs to the start or end overlap of the activity. The following figure illustrates, for instance, the situation where an activity is completely processed inside a break.

For more information, see IloActivity::getEndBreakOverlapMin, IloActivity::getEndBreakOverlapMax, IloActivity::getStartBreakOverlapMax, IloActivity::getStartBreakOverlapMin, IloActivity::setEndBreakOverlapMin, IloActivity::setEndBreakOverlapMax, IloActivity::setStartBreakOverlapMax, IloActivity::setStartBreakOverlapMin.

Each activity may be associated with a set of possibly overlapped at start (resp. end) break types. It means that every break B whose type belongs to this set will be possibly overlapped by the start (resp. end) of the activity.

Any break whose type does not belong to the set of possibly overlapped at start (resp. end) break types cannot be overlapped by the start (resp. end) of the activity. That is, the value of its start (resp. end) overlap is 0.

By default, these sets of possibly overlapped breaks are empty so that no break can be overlapped by the start or end of an activity.

As soon as an activity is associated with a non-empty set of breaks possibly overlapped at start (resp. end), and unless stated otherwise, the activity may overlap these breaks without limitation on the start (resp. end) overlap duration. The functions that allow you to constrain this start (resp. end) overlap duration are the ones listed in Start/End Overlap.

For more information, see IloActivity::addStartBreakOverlapType, IloActivity::removeStartBreakOverlapType, IloActivity::addEndBreakOverlapType, IloActivity::removeEndBreakOverlapType.

As described in the calendar object semantic, the efficiency part of the calendar allows you to model complex dependencies between the activity variables. The relation between start, end and processing time is defined by:

Data regarding the description of the efficiencyCurve are stored in an instance of IloGranularFunction. This object primarily consists of a step-wise integer-to-integer function plus two additional parameters: the granularity and the rounding mode.

Consider for example, the preceding efficiency curve of the required resource R of activity A which has a processing time equal to 4. If the activity starts at time 3, then the activity ends at time 12 (note that in case of downward rounding mode the activity ends in 11 -- see Rounding, Inward & Outward). The duration is then 9. But when it starts in 16, the activity ends in 21 (even with downward rounding mode) and then its duration equals 5.

The efficiency part of the calendar constraint is a special case of the integral constraint (see Functional and Integral Constraints on Resources). Nevertheless this is the only way to safely constrain the processing time variable with an integral behavior when a calendar is used.