Tabella 1

Per effettuare questo test si sono utilizzate macchine il più possibile simili in prestazioni (sparcstation5 per il test effettuato sul sistema operativo Solaris e PentiumII 233Mhz per il test effettuato sul sistema operativo NT) e si è impostato ad un valore comune il parametro "carico di default". Inoltre, durante il test, sulle macchine non erano attivi altri programmi "pesanti" oltre a DFG. In questo modo si è cercato di eliminare possibili fattori esterni che potessero influenzare il risultato del test e quindi le valutazioni che da questo si possono ricavare. I valori riportati nelle tabelle sono la media di una serie di rilevazioni tutte effettuate nelle stesse condizioni.
Tabella 1

Osservazioni:
Si è effettuato il calcolo di una serie di immagini diverse non
solo nel loro costo (stimato), ma anche per le loro caratteristiche intrinseche,
che ne determinano la reale complessità di calcolo. Ad esempio,
le immagini 3 e 4 hanno lo stesso
valore di costo, ma in realtà i punti dell'immagine
4 richiedono un numero di iterazioni mediamente molto superiore per
essere calcolati (ved. Tabella 1).
Tra queste caratteristiche è importante segnalare il grado di
"simmetria" della complessità dell'immagine, che determina l'efficienza
con cui il carico ad essa relativo viene ripartito tra gli slaves disponibili.
Infatti, il tempo richiesto da un calcolo è dato dallo slave che
impiega più tempo per calcolare la sua porzione di immagine. Per
questo motivo, un'errata ripartizione del carico fa sì che molti
slaves terminino il loro lavoro molto prima di altri, determinando così
un drastico calo nelle prestazioni globali del sistema.
Questa considerazione mette in risalto il fatto che per un buon uso delle risorse è necessario impegnare in continuazione tutti gli slaves disponibili. Solo in questo modo è possibile ottenere prestazioni significativamente superiori a quelle ottenibili con un sistema concentrato. In altre parole, il programma DFG non è adatto a calcolare singole immagini, ma a svolgere il calcolo di un numero elevato di immagini contemporaneamente.
Esaminando i dati, si nota subito il fatto che DFG, quando c'è un solo slave a disposizione, è sempre più lento di MandC. Questo è ovviamente causato dall'overhead dovuto alla comunicazione tra le entità che costituiscono DFG.
All'aumentare del numero di slaves disponibili, il tempo di calcolo
generalmente diminuisce. Questo però non accade sempre. Si consideri
l'immagine 5: il tempo necessario per calcolarla è
di soli 25.8sec con due slaves a disposizione, mentre è di 36.3sec
con tre slaves. Questo è dovuto al fatto che questa immagine è
fortemente asimmetrica per quanto riguarda la complessità di calcolo.
La si può infatti suddividere in tre fasce orizzontali, delle quali
quella centrale è estremamente più complessa da calcolare
delle altre.
Per questo motivo, quando si utilizzano tre slaves, due di questi terminano
molto in fretta il proprio compito, mentre il rimanente impiega molto più
tempo. Se invece si utilizzano due slaves l'utilizzo delle risorse è
molto migliore (i due slaves terminano di calcolare quasi contemporaneamente).
Nota: E' possibile introdurre ottimizzazioni nella funzione di calcolo dell'insieme di Mandelbrot in modo da ridurre al minimo le disomogeneità alle quali si è accennato. La versione attuale di DFG non adotta alcun tipo di ottimizzazione. L'introduzione di questo tipo di ottimizzazione migliorerebbe notevolmente le prestazioni globali del sistema, sia perchè ridurrebbe il numero di iterazioni necessarie a riconoscere i punti appartenenti all'insieme di Mandelbrot, sia perchè permetterebbe una più equa ripartizione del carico tra gli slaves.
Un'altra osservazione importante che si può fare osservando i dati è che il sistema fornisce prestazioni migliori nel calcolo di immagini che hanno un costo molto elevato, perchè nel calcolo di tali immagini l'overhead introdotto dalla comunicazione costituisce una percentuale molto piccola del tempo di risposta totale. Infatti, il miglioramento ottenuto nel calcolo dell' immagine più costosa in assoluto passando da uno a cinque slaves è del 74.9% (immagine 4), mentre i miglioramenti ottenuti per le altre immagini vanno dal 47.2% al 58.3%.
Il grafico seguente riporta i dati della Tabella 1:
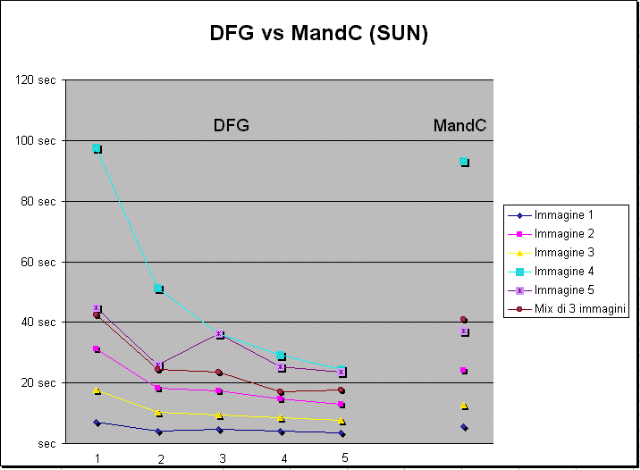
Di seguito sono riportati i tempi ottenuti sul sistema operativo Windows
NT. In queste prove, il miglioramento delle prestazioni dovuto all'utilizzo
di un numero di slaves maggiore è più marcato. Passando da
uno a 4 slaves, il miglioramento va dal 54.9% (per l'immagine1,
che essendo poco costosa risente maggiormente dell'overhead della comunicazione)
al 76.3% (per le immagini 4 e 5,
che sono le più costose e quindi risentono meno dell'overhead della
comunicazione).
Tabella 2

Grafico 2
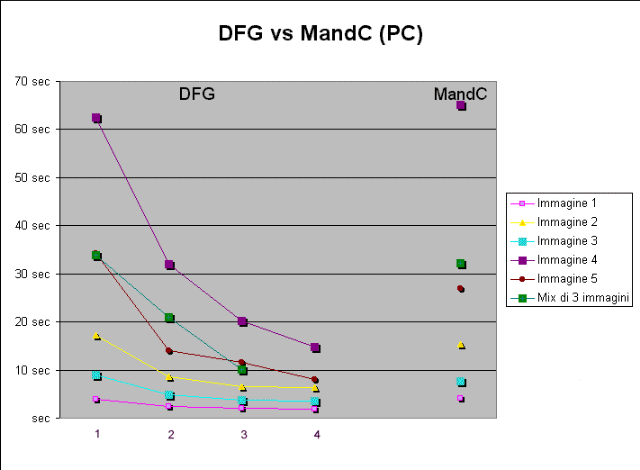
Le caratteristiche delle immagini calcolate sono le seguenti:
| IMMAGINE 1 | ||||||||||||||||||||
|
||||||||||||||||||||
 |
| IMMAGINE 2 | ||||||||||||||||||||
|
||||||||||||||||||||
 |
| IMMAGINE 3 | ||||||||||||||||||||
|
||||||||||||||||||||
 |
| IMMAGINE 4 | ||||||||||||||||||||
|
||||||||||||||||||||
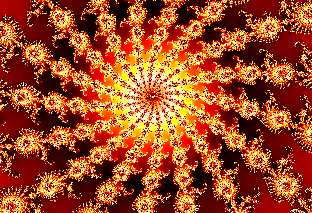 |
| IMMAGINE 5 | ||||||||||||||||||||
|
||||||||||||||||||||
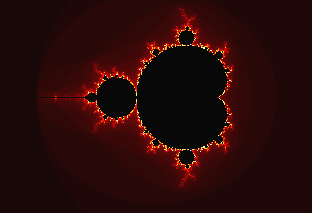 |
| MIX di tre immagini | ||||||
|