DFG - Calcolo dell'insieme di Mandelbrot

L'insieme di Mandelbrot: come viene calcolato da DFG

L'insieme di Mandelbrot è l'insieme dei punti C del piano complesso per i quali non è divergente la serie definita dalla legge ricorsiva

Z_n = Z_n-1²+ C , Z₀ = 0

Iterando la formula per ogni punto del piano complesso, è quindi possibile suddividere i punti in due categorie:

punti che appartengono all'insieme di Mandelbrot
punti che non appartengono all'insieme di Mandelbrot

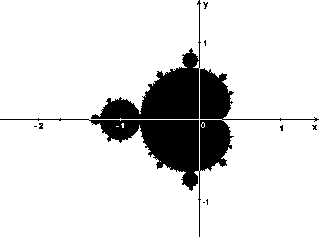Nella figura seguente, i punti dell'insieme di Mandelbrot sono stati colorati di nero: Insieme di Mandelbrot B/N

I valori Z_n ottenuti dal processo di iterazione descrivono un percorso (chiamato "orbita") sul piano complesso. E' quindi possibile immaginare il procedimento di calcolo con cui si verifica l'appartenenza di un punto C all'insieme come la costruzione dell'orbita del punto C e la sua osservazione:

se l'orbita va all'infinito significa che la serie diverge e quindi C non appartiene all'insieme.
se l'orbita non va all'infinito significa che la serie non diverge e quindi che C appartiene all'insieme.

E' ovviamente impossibile calcolare un'orbita completa, perchè questa è costituita da un numero infinito di punti Z_n e quindi richiederebbe un numero infinito di iterazioni per essere calcolata. Fortunatamente, è possibile dimostrare che se il modulo di Z_ndiventa superiore a 2 (vale a dire se l'orbita esce dal cerchio centrato nell'origine di raggio 2), allora l'orbita diverge.
Grazie a questo risultato, è possibile riconoscere i punti che non appartengono all'insieme perchè la loro orbita, dopo un certo numero di iterazioni, esce dal cerchio di raggio 2. Purtroppo, può essere necessario un numero di iterazioni molto elevato prima che l'orbita di un punto non appartenente all'insieme esca dal cerchio. Nel caso di punti appartenenti all'insieme, l'orbita non esce mai dal cerchio, nemmeno dopo un numero infinito di iterazioni. Per questo motivo si fissa un numero massimo di iterazioni, dopo le quali si assume che se l'orbita non è ancora uscita dal cerchio allora non ne uscirà mai e quindi il punto considerato fa parte dell'insieme di Mandelbrot.

E' anche possibile assegnare un colore ai punti che non appartengono all'insieme di Mandelbrot. Esistono molti modi per farlo: il più semplice è detto "metodo del tempo di fuga" e consiste nell'assegnare ai punti un colore che dipende dal numero di iterazioni che sono necessarie per capire che non appartengono all'insieme.

Si può dare una spiegazione intuitiva del nome di questo metodo: si immagini che tutti i punti del piano siano attratti sia dall'insieme di Mandelbrot che dalla retta impropria. E' quindi facile capire perchè i punti più vicini all'insieme abbiano orbite che sfuggono all'infinito più lentamente di quelle relative a punti più lontani dall'insieme.
In quest'ottica, il colore dei punti può essere interpretato come il tempo impiegato dalla loro orbita per sfuggire all'attrazione dell'insieme di Mandelbrot e corrisponde ad una stima della velocità con cui l'orbita diverge.

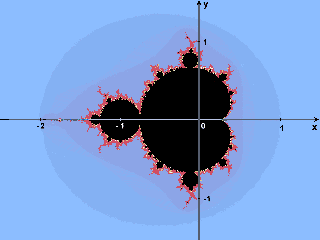
La funzione nativa utilizzata nel programma DFG ha il compito di assegnare un colore ad ogni punto di un'area rettangolare del piano complesso (rappresentata da un array di interi).

Per quanto appena detto, le operazioni svolte dalla funzione per ogni punto C dell'immagine sono le seguenti:

Iterazione della formula Z_n = Z_n-1²+ C partendo dal valore iniziale Z₀= 0.
Se il modulo di Z_n diventa maggiore di 2, allora C non appartiene all'insieme. Il colore da assegnargli dipende dal numero di iterazioni effettuate (n). Dato il valore n, la funzione ottiene i valori RGB del colore da assegnare al punto richiamando un metodo di una sottoclasse della classe Palette.
Se dopo N_MAX iterazioni il modulo di Z_n non è ancora diventato maggiore di 2, allora si assume che C appartenga all'insieme e lo si colora di nero.

Osservazione: le immagini vengono memorizzate nel sistema in formato "grezzo" sotto forma di array di interi a 32bit. La loro occupazione di memoria è quindi notevole, pari a: altezza*larghezza*4 bytes.
Un possibile miglioramento delle prestazioni globali del sistema consiste nell'utilizzare BYTE (che occupano solo 1byte) al posto di INT, ottenendo così un'occupazione di memoria per un'immagine pari a un quarto di quella attuale. Questo è possibile se si trasferisce il compito di trasformare n in una tripla RGB dai DFGSlave al DFGClient. In altre parole, i DFGSlave si limitano a riempire un array di BYTE con valori del tipo n%256, che permettono al client, tramite l'utilizzo di una sottoclasse della classe Palette, di risalire alla tripla RGB di ciascun punto dell'immagine.
Questo metodo presenta anche il vantaggio di rendere inutile l'inserimento della palette da utilizzare per la generazione dell'immagine tra i parametri di Messaggio_Mandelbrot, diminuendone fortemente le dimensioni.

Esempi:
Vediamo come assegnare un colore ad un punto. Iniziamo col considerare un punto al di fuori dell'insieme di Mandelbrot:
C = -0.5 + i.
L'iterazione della formula Z_n = Z_n-1² + C produce i seguenti valori di Z_n: (l'immagine mostra i punti corrispondenti sul piano complesso).

Passo #	Valore_Corrente	Distanza dall'origine
1	-0.5 + i	1.12
2	-1.25	1.25
3	1.06 + i	1.46
4	-0.37 + i * 3.1	3.15

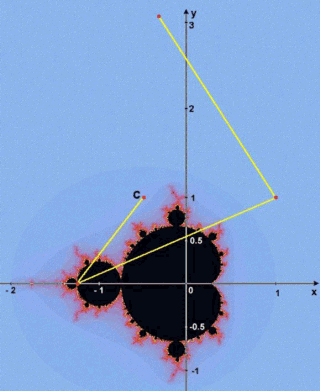Alla terza iterazione, il modulo di Zn diventa maggiore di 2. Questo significa che C non appartiene all'insieme di Mandelbrot. Dato che il numero di iterazioni che sono state necessarie per determinarlo è 3, al punto C viene assegnato il colore n.3 della palette.

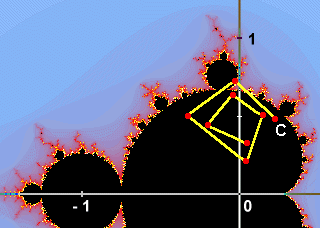
Ripetiamo il procedimento con un punto appartenente all'insieme di Mandelbrot: C = 0.2 + i * 0.5. In questo caso, il modulo di Zn non diventerà mai maggiore di 2 per nessun valore di n. Quando viene raggiunto il numero massimo di iterazioni, si assume che C appartenga all'insieme di Mandelbrot e lo si colora di nero.

Passo #	Valore_Corrente	Distanza dall'origine
1	0.2 + i * 0.5	0.54
2	-0.01 + i * 0.7	0.7
3	-0.29 + i * 0.49	0.57
4	0.05 + i * 0.22	0.22
5	0.15 + i * 0.52	0.54
6	-0.05 + i * 0.66	0.66
7	-0.23 + i * 0.44	0.48
8	0.06 + i * 0.3	0.3
. .	. . . . . . . . . . . .	. . . .

Per maggiori informazioni sull'insieme di Mandelbrot: Fractal Explorer