Solve
 PREVIOUS
NEXT
PREVIOUS
NEXT
| IBM ILOG Solver User's Manual > More on Solving > Limits and Problem Decomposition: Locating Warehouses > Solve |
Solve |
INDEX
 PREVIOUS
NEXT
PREVIOUS
NEXT
|
In this lesson, you will learn how to decompose a problem and how to set limits on the search. Using this approach, Solver will not search the entire search tree and it may miss an optimal solution. However, Solver will explore a more promising part of the search tree more quickly. You will also learn how to use another search strategy--Depth-Bounded Discrepancy Search (DDS).
In Chapter 13, Controlling the Search: Locating Warehouses, you created goals for three decision variables: cost, supplier, and totalCost. These three goals were combined into one goal. You then applied a node evaluator to this combined goal. In the search, you used a search selector created from the totalCost variable.
In this lesson, you do not combine the goals at first. You apply node evaluators to the goals individually. You add a search limit to the first goal you execute. In the first phase, you search the search tree with a goal created from the cost variable. You prune the search tree based on a search limit associated with this goal. In the second phase, you search the remaining part of the search tree with a goal created from the supplier variable. In both phases of the search, you use a search selector created from the totalCost variable.
You will perform eight steps to create a final goal to be used in search:
IloGenerate to return goal1 for the decision variable cost.
IloApply. This function applies the node evaluator IloDDSEvaluator to goal1 and returns applygoal1.
IloLimitSearch. This function places a fail limit on applygoal1 and returns limitgoal1.
IloGenerate to return goal2 for the decision variable supplier.
IloApply. This function applies the node evaluator IloSBSEvaluator to goal2 and returns applygoal2.
combinedGoal by joining the following goals with logical AND operators: limitgoal1, applygoal2, and a goal returned by the function IloInstantiate for the variable totalCost. Goals that are combined with logical AND operators are executed in the order they are declared--from left to right.
minimizeSearchSelector, from the totalCost variable. The objective, which is to minimize the total cost, is treated implicitly by the search selector.
IloSelectSearch. This function takes combinedGoal and minimizeSearchSelector as parameters and returns finalGoal.
The member function IloSolver::solve takes finalGoal as a parameter and searches for a solution in two phases. In the first phase, Solver searches using the goal limitgoal1. The search tree is pruned by this goal. In the second phase, the remaining part of the search tree is searched using applygoal2 until a solution is found. The search selector minimizeSearchSelector is used in both phases of the search. Figure 14.1 demonstrates this procedure.
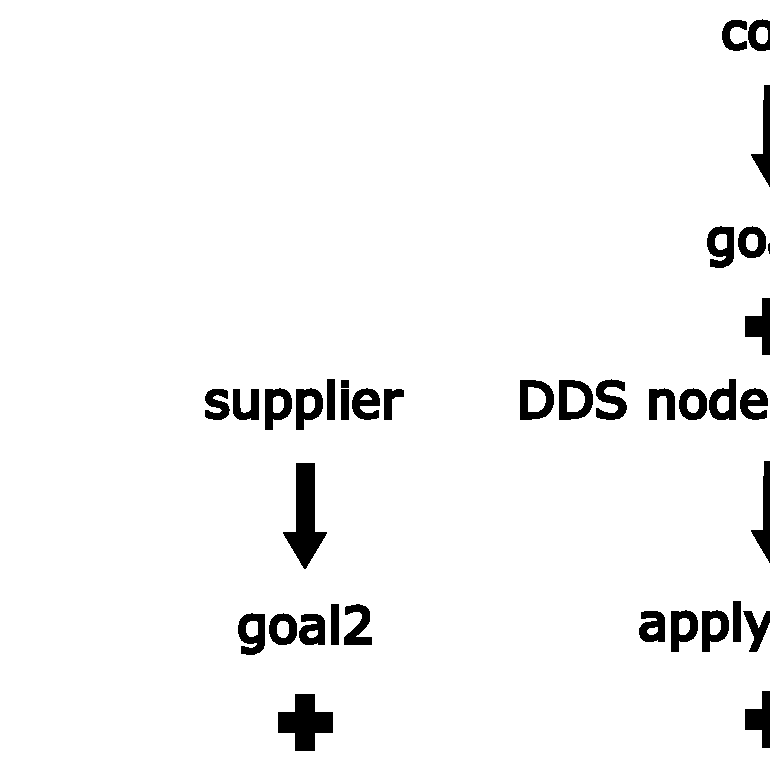
To start, you use the function IloGenerate to return goal1 for the decision variable cost. You use the parameter IloChooseMaxRegretMin for the array of variables cost. This parameter uses the principle of least regret to guide the search strategy. For more information on IloChooseMaxRegretMin, see the section "Solve".
Step 2 - | Create goal1 |
Add the following code after the comment //Create goal1
IloGoal goal1 = IloGenerate(env, cost, IloChooseMaxRegretMin); |
Now, you apply a node evaluator to goal1. In this lesson, you apply a node evaluator that implements Depth-Bounded Discrepancy Search (DDS). DDS makes the assumption that mistakes are more likely near the top of the search tree rather than further down. For this reason, this procedure does not count the number of discrepancies but the depth of the last one.
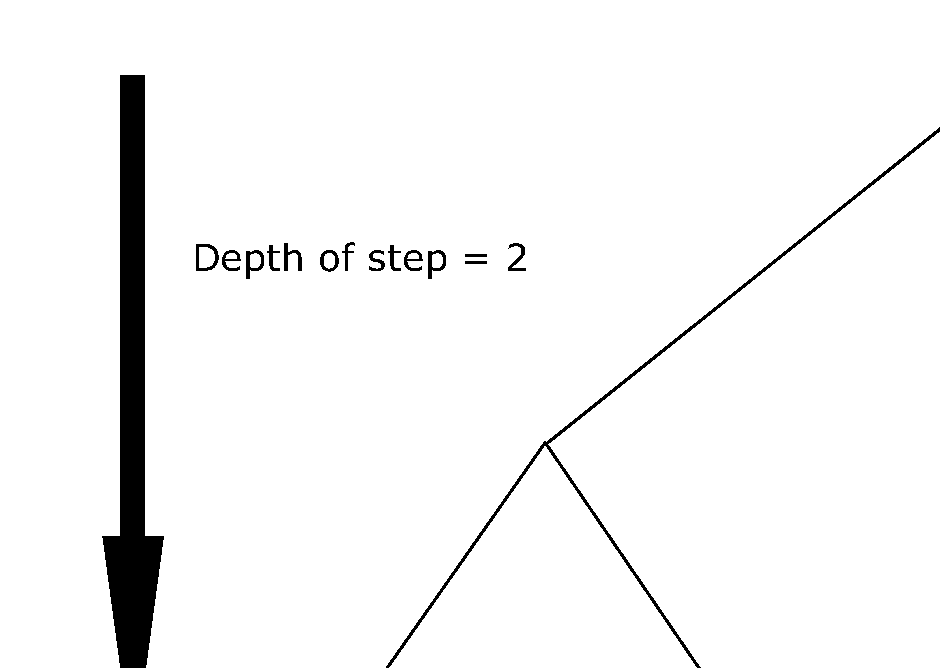
The function IloDDSEvaluator creates and returns an instance of IloNodeEvaluator that implements Depth-Bounded Discrepancy Search. The first parameter is the environment. The second parameter step. Solver will first explore nodes with a depth less than step. After this exploration is complete, it will explore nodes with a depth between step and 2 * step, and so on. The third parameter is width. Solver will look first at paths, starting from the depth level, that have a number of discrepancies, or right moves, less than or equal to width. The fourth parameter is maxDiscrepancy. If this parameter is used, Solver will discard nodes with a number of discrepancies greater than maxDiscrepancy. The default value for maxDiscrepancy is IloIntMax, which means that Solver will not discard any nodes based on this parameter. Here is a constructor:
IloNodeEvaluator IloDDSEvaluator(IloEnv env, IloInt step = 4, IloInt width = 2, IloInt maxDiscrepancy = IloIntMax); |
Figure 14.2 shows a search tree that has been traversed with a node evaluator that implements Depth-Bounded Discrepancy Search (DDS) with a depth of 2 and a width of 1. The numbers in the first row represent the order in which paths are evaluated. As you can see, Solver first evaluates paths 1, 2, and 3. It then jumps to paths 4, 5, and 6. It then jumps to paths 7, 8, and 9, and so on. The numbers in the second row represent the number of discrepancies, or right moves, in each path after the level of depth 2. This is called the width. As you can see, Solver first search the paths with 0 or 1 discrepancy and then the paths with 2 discrepancies.
You now use the function IloApply. This function applies the node evaluator IloDDSEvaluator to goal1 and returns applygoal1. The node evaluator will first search paths in the search tree with a depth of 3 or less nodes. It will search paths deeper than this depth that have a number of discrepancies, or right moves, less than or equal to 1.
Step 3 - | Create applygoal1 |
Add the following code after the comment //Create applygoal1
IloGoal applygoal1 = IloApply(env, goal1, IloDDSEvaluator(env, 3, 1)); |
Now, you will apply a search limit to the goal applygoal1. You will use the function IloFailLimit to limit the search after maxNbFails failures have occurred. Here is a constructor:
IloSearchLimit IloFailLimit(IloEnv env, IloInt maxNbFails); |
Now, you use the function IloLimitSearch. It takes three parameters: the environment, a goal, and a search limit. This function places a fail limit on applygoal1 and returns limitgoal1. The fail limit stops the search after 5 failures have occurred.
Step 4 - | Create limitgoal1 |
Add the following code after the comment //Create limitgoal1
IloGoal limitgoal1 = IloLimitSearch(env, applygoal1, IloFailLimit(env, 5)); |
You use the function IloGenerate to return goal2 for the decision variable supplier.
Step 5 - | Create goal2 |
Add the following code after the comment //Create goal2
IloGoal goal2 = IloGenerate(env, supplier); |
You now use the function IloApply. This function applies the node evaluator IloSBSEvaluator to goal2 and returns applygoal2. This node evaluator will first search paths in the search tree with 1 or less discrepancies, or right moves. It will also discard nodes with a number of discrepancies greater than or equal to 1. For more information on the node evaluator IloSBSEvaluator, see the section "Solve" in Chapter 13, Controlling the Search: Locating Warehouses.
Step 6 - | Create applygoal2 |
Add the following code after the comment //Create applygoal2
IloGoal applygoal2 = IloApply(env, goal2, IloSBSEvaluator(env, 1, 1)); |
Next, you create combinedGoal by joining the following goals with logical AND operators: limitgoal1, applygoal2, and a goal returned by the function IloInstantiate for the variable totalCost.
Step 7 - | Create the combinedGoal |
Add the following code after the comment //Create the combinedGoal
IloGoal combinedGoal = limitgoal1 && applygoal2 && IloInstantiate(env, totalCost); |
Then, you create a search selector, minimizeSearchSelector, from the totalCost variable. This search selector stores the leaf of the search tree that represents a solution with the optimal value of the variable totalCost. After the search tree has been completely explored, it reactivates this value. When a solution is found, it adds a constraint that totalCost must be less than or equal to the solution minus 1.
Step 8 - | Create the search selector |
Add the following code after the comment //Create the search selector
IloSearchSelector minimizeSearchSelector = IloMinimizeVar(env, totalCost, 1); |
Finally, you use the function IloSelectSearch. This function takes combinedGoal and minimizeSearchSelector as parameters and returns finalGoal. It applies the search selector minimizeSearchSelector to the goal combinedGoal.
Step 9 - | Create the finalGoal |
Add the following code after the comment //Create the finalGoal
IloGoal finalGoal = IloSelectSearch(env, combinedGoal, minimizeSearchSelector); |
Now, you create an instance of IloSolver to solve the problem expressed in the model. This code is provided for you:
IloSolver solver(model); |
You use the member function IloSolver::solve to search for a solution. You use finalGoal as a parameter of IloSolver::solve.
Step 10 - | Search for a solution |
Add the following code after the comment //Search for a solution
if (solver.solve(finalGoal)) |
Step 11 - | Compile and run the program |
Compile and run the program. You should get the following results, though the information displayed by IloSolver::printInformation will vary depending on platform, machine, configuration, and so on:
As you can see, the solution is the same as that found in Chapter 13, Controlling the Search: Locating Warehouses. However, there are fewer fails and fewer choice points. Using problem limits and decomposition, there are only 5 fails and 10 choice points, as opposed to 25 fails and 27 choice points using slice-based search without problem limits and decomposition.
The complete program is listed in "Complete program". You can also view it online in the file YourSolverHome/examples/src/storecpx.cpp.
IBM® ILOG® Solver Search StrategiesDepth-First Search (DFS)
DFS is the standard search procedure. Depth-First Search explores the search tree in a "left-to-right" fashion. It searches by selecting the left leaf at each open node until the end of the search space is reached. If it does not find a solution, it backtracks and tries again. The function Best First Search (BFS)
BFS is described in N. J. Nilsson's book, Problem Solving Methods in Artificial Intelligence, published by McGraw-Hill, 1971. The Solver implementation uses a parameter Slice-Based Search (SBS)
SBS is described by J. Christopher Beck and Laurent Perron in their paper, "Discrepancy Bounded Depth First Search," presented at the Second International Workshop on Integration of AI and OR Technologies for Combinatorial Optimization Problems (CP-AI-OR'00), Paderborn, Germany, 2000. The discrepancy of a search node is defined as the number of right moves. Given a parameter step, slice-based search will first explore nodes with a discrepancy less than step. After this exploration is complete, it will explore nodes with a discrepancy between step and 2*step, and so on. This search strategy cuts the search tree into slices. The function Depth-Bounded Discrepancy Search (DDS)
DDS was introduced by Toby Walsh in his paper, "Depth-Bounded Discrepancy Search," published in the Proceedings of the International Joint Conference on Artificial Intelligence (IJCAI), volume 2, August, 1997, pages 1388-1393. DDS makes the assumption that mistakes are made more likely near the top of the search tree than further down. For this reason, this procedure does not count the number of discrepancies but the depth of the last one. Solver implements an improved version of Walsh's schema. Given a parameter step, DDS will first explore nodes with a depth less than step. After this exploration is complete, it will explore nodes with a depth between step and 2*step, and so on. Solver's implementation of DDS takes a parameter width, that allows width number of discrepancies beyond the depth specified by the parameter step. The function Interleaved Depth-First Search (IDFS)
IDFS was introduced by Pedro Meseguer in his paper, "Interleaved Depth-First Search," published in the Proceedings of the International Joint Conference on Artificial Intelligence (IJCAI), volume 2, August, 1997, pages 1382-1387. IDFS tries to mimic the behavior of an infinite number of threads exploring the search tree. Solver implements a variation that limits the depth of this behavior. The function |
| © Copyright IBM Corp. 1987, 2009. Legal terms. | PREVIOUS NEXT |