Suppose we have a scheduling problem that consists in scheduling n activities with different durations on a single unary resource.

Suppose also that we have a set of additional constraints that state some minimal delays between the activity scheduled at position i and the one scheduled at position j (regardless of which activities will be scheduled at these positions). More precisely, we have a set of m additional constraints C(i, j, d) where i, j in [0, n], i < j, d > 0. Let's suppose that in a solution, the activities are ranked at positions 0 ,..., n-1. Constraint C(i, j, d) states that between the start of the activity ranked at position i and the start of the activity ranked at position j, there should be at least a delay d.

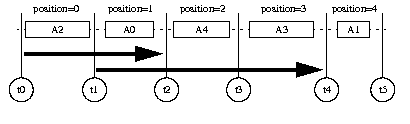
The problem consists of finding an order between the activities on the unary resource that satisfies all constraints, C(i, j, d), and minimizes the makespan.