Define the RoutingSolver constructor

IBM ILOG Dispatcher User's Manual > The Basics > Solving a Vehicle Routing Problem > Solve > Define the RoutingSolver constructor

Define the RoutingSolver constructor

INDEX

PREVIOUS NEXT

The constructor takes an instance of RoutingModel as a parameter. The environment, model, solver, dispatcher, and solution are initialized. This constructor will be called from the main function. The following code is provided for you:

 RoutingSolver::RoutingSolver(RoutingModel mdl):
  _env(mdl.getEnv()),
  _mdl(mdl.getModel()),
  _solver(mdl.getModel()),
  _dispatcher(_solver),
  _solution(mdl.getModel()){

Next, the three goals used in the search for a solution are created.

Step 2 -

Create the goal to instantiate cost

Add the following code after the comment //Create the goal to instantiate cost

     _instantiateCost =
          IloDichotomize(_env, _dispatcher.getCostVar(), IloFalse);

You use the function IloDichotomize to instantiate the cost variable to its minimum value--Dispatcher's constraints only provide a lower bound on the cost. The cost variable is returned by the member function IloDispatcher::getCostVar. This variable is the sum of the cost of the vehicles and of the unperformed visits. The function IloDichotomize creates a goal which attempts to assign a value to the variable. To do so, it recursively searches half the domain of the variable at a time. Since you are minimizing the cost variable, you set the last parameter to IloFalse, which tries the lower half of the domain first.

Next, you create the goal to restore the solution.

Step 3 -

Create the goal to restore the solution

Add the following code after the comment
//Create the goal to restore the solution

      _restoreSolution = IloRestoreSolution(_env, _solution);

This goal will be used in the solution improvement phase. Solver will try to iteratively improve the solution. The last solution found will be the lowest cost solution. You will then restore this last solution using the goal _restoreSolution.

Now, you create the goal to find a first solution.

Step 4 -

Create the goal to find a first solution

Add the following code after the comment
//Create the goal to find a first solution

     _goal = IloSavingsGenerate(_env) && _instantiateCost;
  }

You use the savings heuristic to create a first solution using the predefined function IloSavingsGenerate. Figure 3.1 shows how the savings generation heuristic works. For problems with multiple vehicles, it is very important to consider the trade-off between more vehicles with shorter routes and fewer vehicles with longer routes. For example, the following figure shows two ways of making visits a and b.

Figure 3.1 The Savings Generation Heuristic

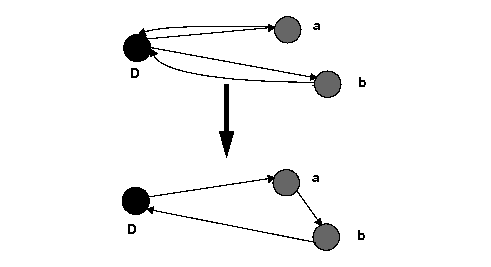
The savings of serving a and b in the same route, denoted savings (a, b), is defined as savings (a, b) = cost (a, Depot) + cost (Depot, b) - cost (a, b). The savings heuristic generates a solution based on this equation.

You can use other predefined heuristics to find a first solution including: sweep, nearest-to-depot, nearest addition, insertion, and enumeration heuristics. For more information on predefined first solution heuristics, see ïtò^ A Predefined First Solution Heuristics. The first solution can also be loaded from a file or you can write your own first solution heuristic. For more information, see Chapter 17, Developing Your Own First Solution Heuristics.

After the heuristic finds a first solution, you use the goal _instantiateCost to find the cost associated with this solution.

PREVIOUS NEXT