This section presents the implementation of the constraints of this problem according to the second model. It uses the following notation:

Constraint: Number of cards

The first constraint states that the number of cards plugged into a rack is less than or equal to its number of connection slots.

For each rack a,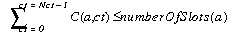

Constraint: Power used

The power used by the cards plugged into rack a must be less than or equal to the maximal power it provides.

Generic constraints and class constraints

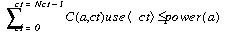
Those two constraints--number of cards and power used--are implemented directly by the functions IloSum and IloScalProd. These are both generic constraints predefined in the Solver library. By generic, it is meant that a single constraint applies to a number of constrained variables simultaneously. Those two constraints are added by the constructor of the class Rack. In other words, you are using those two generic constraints as class constraints. The constructor uses the following code:

Rack::Rack(IloModel model, IloIntArray cardPower) {
  IloEnv env = model.getEnv();
  _type = IloIntVar(env, 0, nbRackTypes);
  _counters = IloIntVarArray(env, nbCardTypes, 0, maxSlots);
  _price = IloIntVar(env, 0, 10000);
  IloIntArray prices(env, nbRackTypes + 1);
  IloIntArray rackPower (env, nbRackTypes + 1);
  IloIntArray rackSlot (env, nbRackTypes + 1);
  for (IloInt i=0; i<nbRackTypes + 1; i++) {
    prices[i] = Racks[price][i];
    rackPower[i] = Racks[power][i];
    rackSlot[i] = Racks[nbSlot][i];
  }
  model.add(_price ==  prices(_type));
  model.add(IloScalProd(_counters, cardPower) <= rackPower(_type));
  model.add(IloSum(_counters) <= rackSlot(_type));
}

In that code,

The construction T[i] = v (where T is an instance of IloNumVarArray, and i and v are instances of IloNumVar) constrains the ith element of T to be equal to v. The code of the Rack constructor also shows other ways to use this element constraint.

Constraint: Demand

To make sure that all cards of a given type are used, you state that the sum of all counters of this card type associated with the racks is equal to the given number of those cards:

For each card type ct,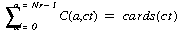

This constraint is implemented by the function IloSum, a predefined generic constraint that applies simultaneously to a number of constrained variables. It is added in the main function.

    // all cards must be plugged
    for(j = 0; j < nbCardTypes; j++){
      IloIntVarArray vars(env,nbRack);
      for(i = 0; i < nbRack; i++)
        vars[i] = racks[i]->_counters[j];
      model.add(IloSum(vars) == nbCards[j]);
    }

Redundant constraint: Eliminating more symmetry

This model still has a lot of symmetries: any permutation between racks gives a new "solution." You remove these symmetries by defining an order among the configurations of each rack. The idea is to state that the type of rack i-1 is greater than the type of rack i. This order constraint removes some symmetries.

That redundant constraint is stated like this in the main function:

    // remove symmetries
    for(i = 1; i < nbRack; i++){
      model.add(racks[i]->_type >= racks[i-1]->_type);
      model.add(IloIfThen(env, racks[i-1]->_type == racks[i]->_type,
                               racks[i-1]->_counters[0] <= racks[i]-
>_counters[0]));
    }