Solve
 PREVIOUS
NEXT
PREVIOUS
NEXT
| IBM ILOG Solver User's Manual > More on Solving > Setting Filter Levels: Coloring Graphs > Solve |
Solve |
INDEX
 PREVIOUS
NEXT
PREVIOUS
NEXT
|
After you have declared the variables and added the constraints to the model, you are ready to search for a solution. In this lesson, you will not actually display the solution to the graph coloring problem, but instead search to see if a solution is possible. You will learn how to time a search and how to use different filter levels for constraints.
First you create an instance of the class IloSolver to solve the problem expressed in the model. This code is already provided for you:
IloSolver solver(model); |
Now, you create an instance of the class IloTimer. This class works like a stop watch and you will use it to time how long it takes to find a solution to the graph coloring problem using different filter levels.
Step 6 - | Create the timer |
Add the following code after the comment //Create the timer
IloTimer timer(env); |
Now, you set filter levels for constraints. Constraint propagation is, of course, more sophisticated than discussed in the introductory section "Solve" in Chapter 1, Constraint Programming with IBM ILOG Solver. Each constraint is associated with a filtering algorithm. This filtering algorithm performs domain reductions based on the associated constraint--it will remove values from the current domains of variables that do not belong to a solution. Constraint propagation is the mechanism used to communicate the effects of these domain reductions.
For some types of constraints, you can set a filter level that specifies the type of filtering algorithm. So far, you have looked at two types of constraints. These are:
x != y, that affect two variables
IloAllDiff and IloDistribute, that can be defined as a set of non-global constraints
For all constraints except global constraints, the filtering algorithm is always the same. For global constraints, the filtering algorithm varies depending on the filter level. There are three filter levels for global constraints: IloBasicLevel, IloMediumLevel, and IloExtendedLevel.
To understand the difference between these filter levels, consider the IloAllDiff global constraint. You can view this constraint in two ways. It can be seen as a set of inequality != constraints or as one global constraint. For example, consider a graph coloring problem with three nodes: x, y, and z. All the nodes must be colored a different color. Node x can be colored red or blue; node y can be colored red or blue; and node z can be colored red, blue, or yellow. If you set the filter level of IloAllDiff to IloBasicLevel, the filtering algorithm treats this global constraint as a set of inequality constraints. Looking at each set of binary constraints individually, the filtering algorithm is not able to reduce the domains. The domains are not reduced after constraint propagation and appear as in Figure 12.5.
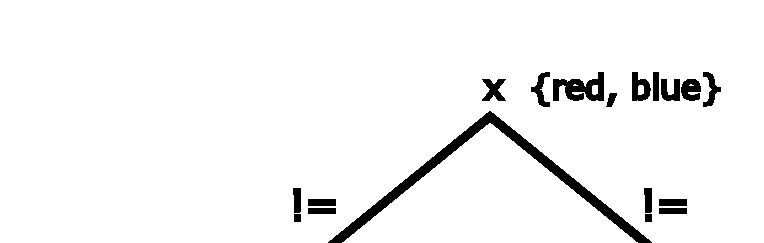
If you set the filter level of IloAllDiff to IloExtendedLevel, the filtering algorithm treats this global constraint as a truly global constraint. The filtering algorithm is not able to reduce the domains of x and y. However, the filtering algorithm can "realize" that between them, variables x and y must use both of the values red and blue. This leaves only the value of yellow available for variable z. The domain of z is reduced after constraint propagation and appears as in Figure 12.6.
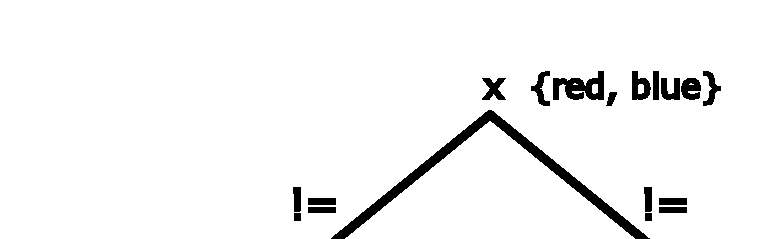
Given that IloExtendedLevel is the most thorough filter level, why would you use any other filter level? There is a tradeoff in using IloExtendedLevel. In general, IloExtendedLevel takes longer. The filter level IloBasicLevel is less thorough, but faster. IloMediumLevel is a compromise between the two levels--faster than IloExtendedLevel and more thorough than IloBasicLevel. However, these are general rules and are not true for every situation. Depending on your application, different filter levels may be appropriate. In this lesson, you run each test of the graph with the three filter levels and include performance output. You can analyze the different results.
You use the member function IloSolver::setDefaultFilterLevel to set the filter levels for all global constraints. This function takes two parameters: the first specifies the type of global constraint, the second specifies the filter level.
Step 7 - | Set the default filter level |
Add the following code after the comment //Set the default filter level
solver.setDefaultFilterLevel(IloAllDiffCt,IloExtendedLevel); |
Now, you use the member function IloTimer::start to start the timer.
Step 8 - | Start the timer |
Add the following code after the comment //Start the timer
timer.start(); |
You search for a solution using the predefined goal IloGenerate. Since you have chosen the parameter IloChooseMinSizeInt, Solver will first choose the unbound variable with the smallest domain and propagate the effects of this move, and so on. If a search move leads to a situation where a constraint is not satisfied, it is undone and Solver backtracks.
Step 9 - | Search for a solution |
Add the following code after the comment //Search for a solution
if (!solver.solve(IloGenerate(env,vars,IloChooseMinSizeInt))) solver.out() << "No solution" << endl; |
When a solution is found, you display the size of the maximal cliques, the number of failures, and the elapsed time. This code is provided for you:
solver.out() << "IloExtendedLevel \t clique size:" << nTest; solver.out() << "\t#fails:\t" << solver.getNumberOfFails() << "\t"; solver.out() << "cpu time: " << timer.getTime() << " s" << endl; |
Now, you add the code to run the tests using the filter levels IloMediumLevel and IloBasicLevel. You will not have the thorough domain reductions that you had using IloExtendedLevel. Therefore, it is a good idea to add a redundant constraint to reduce the search space.
As you remember from Chapter 6, Using the Distribute Constraint: Car Sequencing, the IloDistribute constraint takes three arrays as parameters: cards, values, and vars. The constrained variables in the array cards are equal to the number of occurrences in the array vars of the values in the array values. If no values array is specified, this array is assumed to be an array of consecutive integers starting at 0. More precisely, for each i, cards[i] is equal to the number of occurrences of values[i] in the array vars.
Step 10 - | Add the redundant IloDistribute constraint |
Add the following code after the comment //Add the redundant IloDistribute constraint
IloIntVarArray cards(env,nbColors,nbNodes/nbColors, nbNodes/nbColors); IloConstraint distribute=IloDistribute(env,cards,vars); model.add(distribute); |
Here is an example of how the distribute constraint would work for a graph of size n = 3, with 6 nodes and 3 colors. The array cards consists of 3 elements. The elements all have the same value--the upper and lower bounds are both nbNodes/nbColors, or 6/3 = 2. The array values must be the same size as the array cards, or 3 elements. These are the first three consecutive integers starting at 0 and represent the possible colors. There are 6 variables that represent the color of each node.
In a graph of size n = 3, the array cards is [2, 2, 2]. The array values is [0,1,2]. Therefore, the value 0 (element [0] in the array values) must occur 2 (element [0] in the array cards) times in the array vars. Likewise, the value 1 must occur 2 times and the value 2 must occur 2 times. One possible set of values for the array vars that would satisfy this distribute constraint is [0, 2, 1, 1, 2, 0]. The value 0 occurs 2 times, the value 1 occurs 2 times, and the value 2 occurs 2 times.
| Note |
| This is just an example of a set of values that would satisfy the distribute constraint. It is not necessarily a set of values that would represent a solution to the problem. |
Now you add the default filter level IloMediumLevel. This code is provided for you:
Finally, you run the tests with the default filter level IloBasicLevel. This code is provided for you:
In this example, you model and solve the problem in the function testGraph. The main function only serves as a way to input the clique size of the graph and to call the function testGraph. You run the first test on a graph with a maximal clique size of 27 (378 nodes). The second test is run on a graph with a maximal clique size of 29 (435 nodes). The third test is run on a graph with a maximal clique size of 31 (496 nodes). This code is provided for you:
int main(int argc, char** argv){ IloInt b1=(argc>1)?atoi(argv[1]):27; IloInt b2=(argc>2)?atoi(argv[2]):b1+4; for(IloInt nTest = b1; nTest < b2+1; nTest+=2){ testGraph(nTest); } return 0; } |
Step 11 - | Compile and run the program |
Compile and run the program. You should get the following results:
As you can see, Solver found a solution for the graph coloring problem with test runs of maximal clique size 27, 29, and 31. The number of failures and the time to solve varies depending on the filter level. At these clique sizes, the IloExtendedLevel filter level has fewer failures, but takes longer.
You can experiment by trying different clique sizes. Here is a test run with maximal cliques of size 51, 53, and 55. You can observe that the test run with a clique of size 55 follows the general pattern. There are fewer fails for IloExtendedLevel, but it takes the longest time to solve. However, the test runs of clique size 51 and 53 do not follow the normal pattern. This is because this graph coloring problem does not get more difficult in a purely linear fashion. Certain clique sizes, regardless of relative size, are very difficult to solve. Often these more difficult instances of the problem will solve faster with a filter level of IloExtendedLevel or IloMediumLevel. Here are the results:
The following test run on a clique of size 61--a particularly difficult instance of the problem--demonstrates the importance of trying different filter levels in your problem. You will get the following solutions for the filter levels of IloExtendedLevel and IloMediumLevel. However, you will not have any response about the test using filter level IloBasicLevel for many hours:
-------------------------------------- IloExtendedLevel clique size:61 #fails: 5 cpu time: 22.502 s IloMediumLevel clique size:61 #fails: 120408491 cpu time: 172926 s |
The following test run on a clique size of 71 again demonstrates the general case. The filter level IloBasicLevel is fastest and the filter level IloExtendedLevel is the most thorough, with only 5 fails:
The complete program is listed in "Complete program". You can also view it online in the file YourSolverHome/examples/src/graph.cpp.
| © Copyright IBM Corp. 1987, 2009. Legal terms. | PREVIOUS NEXT |