The type of representation chosen for the solution to a problem can have a great effect both on the genetic operators used and the overall efficiency of the resulting genetic algorithm. Representations fall into two broad categories: direct and indirect. A direct representation is the one that you are most used to dealing with in Solver; it might be referred to as the "natural" representation, and has the benefit that it is easy to evaluate. An indirect representation is one which sits alongside the direct representation and is not complete in itself. In order to evaluate an instantiation in the indirect representation, a decoder or mapping function is invoked which transforms the solution in the indirect representation into one in the direct representation. In the EA framework, the way of doing this is with a constraint programming goal which uses the values of variables in the indirect representation to influence its instantiation of the direct representation. Note that in general there is no one-to-one correspondence between solutions in the two representations. Many solutions in the indirect representation may decode to the same solution in the direct representation. Equally, some directly represented solutions may be impossible to obtain as there may be no solution in the indirect representation which maps to them.

An example of an indirect representation of scheduling is a unique priority for each activity. The description of a possible decoding goal could then be stated as follows. The decoder schedules activities one by one until all activities are scheduled. At each step, among the activities which can be scheduled, the decoder chooses the one with highest priority. This activity is then placed as early as possible in the schedule. Importantly, using constraint programming, this last decision can be backtracked in the case of a failure, and alternative assignments tried. This, combined with constraint propagation, makes decoders written using constraint programming more robust. This will be elaborated on below.

Figures below show the use of a direct and indirect representation in the EA framework.

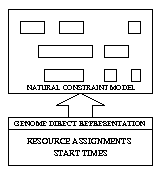
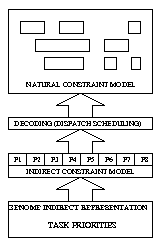
Given its additional complexity, what are the advantages of the indirect representation? First, the indirect representation is normally free of constraints, or has constraints which are easy to satisfy. For example, there may be only "range" constraints on a set of priorities for activities. Thus, matters can be arranged such that any genetic operators applied to a solution in the indirect representation result in a new valid solution. This moves the burden of maintaining feasibility of the direct representation to the decoder. The decoder is then responsible for interpreting the indirect representation, and instantiating the direct representation such that the constraints therein (that is, the original problem constraints) are respected.

At this point an additional question might be posed. Does the indirect representation have any merit when constraint programming is being used? After all, one of the benefits is that constraints in the direct representation are handled directly. This is true, but depending on the problem being addressed, the performance of genetic operators on the direct representation can vary. The problem of finding a solution for a mutation or combination operator on the direct representation is combinatorial in nature. The problem of decoding the indirect representation under constraints is also combinatorial in nature, but importantly is normally easier in practice. Moreover, constraint programming delivers the advantage over traditional methods that additional constraints can be added to the problem without changing the decoder. Constraint propagation and the ability to backtrack bad decisions greatly increase the robustness of decoding.

So, when should you use a direct representation, and when should you use an indirect one? This is not always the easiest question to answer, but some general advice can be given. There are two main reasons for using an indirect representation. The first one is that the problem is strongly coupled. What do we mean by this? One way to think about it is by asking yourself the following question. If I have a solution to my problem (in the direct/natural representation), and I change a small part of this solution, how much of the rest of the solution would I need to change to stay compatible with the initial change? If the answer is "a lot," the problem is strongly coupled. Often the best way to imagine the initial change is as one which needs to be made because a machine breaks down, a time slot becomes unavailable, a road is closed, a delivery is delayed, and so on. You may then ask, "How much of my solution will this change affect?" For example, imagine a scheduling problem where the objective is to minimize the total length of the schedule. Good solutions to such problems tend to be tightly packed and have little "slack." In these types of problems, if some input (say some raw material) arrives late, then this can have huge implications on the schedule; there is seldom a "small fix" which will maintain feasibility. Such problems can be so tightly coupled that small mutations on a direct representation have little hope of working. Even when using constraint programming, the closest legal schedule may be far from what is proposed by the genetic operator, and thus may take an unacceptably long time to find. Contrast this with a schedule where the objective is to minimize labor costs. Such a problem tends to be much more loosely coupled. In this case, if some goods arrive late, then we can normally change the schedule slightly to account for this, for instance by authorizing overtime for a period until the schedule is back on track. The cost will be higher than in the original schedule, but importantly, the schedule only had to be slightly modified. Here, small mutations of the schedule have a much higher probability of resulting in a legal schedule, even if at increased cost.

The second reason why an indirect representation can be preferred to a direct one is probably even more important than the first. Indirect representations are often much more standardized than direct ones. Direct representations are necessarily specific to the problem class, whereas indirect ones tend to center around themes. A common theme is to give a priority to each assignable object in the problem. A decoder then decides what to do with these objects in priority order. The use of standardized indirect representations allow simple (and often built-in) genetic operators to be used. This still means that a decoder needs to be written for the problem class at hand, but this is usually relatively simple. With direct representations on the other hand, genetic operators usually need to be written for the problem class being addressed; normally a much more sophisticated task.

It should be mentioned that with good design of genetic operators made for the problem class at hand, direct representations can be effective even for problems which are quite strongly coupled. Performance in such cases is often significantly better than that of indirect representations as no decoding phase is present. However, the design of hand-crafted operators can be a difficult and painstaking endeavor, and as such, we recommend using an indirect representation as a first step either in the case where no built-in operators match the direct representation of the problem, or where the problem is strongly coupled.