There is really no point in examining all the possible solutions for variables and their values when two or more constrained variables satisfy the following conditions:

In fact, the permutations give rise to sets of solutions that are identical as far as the physical reality of the problem is concerned. We can exploit this idea to minimize the size of the search space.

Principle

If we reduce these domains by introducing a supplementary constraint, such as order, or by imposing a special feature on each of these variables, we can markedly reduce the size of the search space.

Example

Let's assume, for example, that we have the following system of equations:

x1 + x2 + x3 = 9

x1 × x2 × x3 = 12

For the ordered triple (x1, x2, x3), there are six solutions:

(1, 2, 6) (1, 6, 2) (2, 1, 6) (2, 6, 1) (6, 1, 2) (6, 2, 1)

If we permute the variables, the problem is not changed. For instance, if we swap x1 and x2, the problem becomes:

x2 + x1 + x3 = 9

x2 × x1 × x3 = 12

That problem is obviously the same as the first one. In this case, it is a good idea to introduce a supplementary constraint to enforce order among the variables. We can do that in this way:

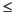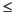x1  x2  x3

Our additional constraint on the order among the variables greatly reduces the combinatorial possibilities without removing any real solutions.

In fact, only one solution can be returned under these conditions:

(x1, x2, x3) = (1, 2, 6)

We also note that the presence of large inequalities in the constraint takes care of the possibility of getting the same value for two or more variables. In our example, that is the effect that we want, but more generally, we have to guard against adding a supplementary constraint that inadvertently suppresses solutions that we would like to see.