Describe
 PREVIOUS
NEXT
PREVIOUS
NEXT
| IBM ILOG Solver User's Manual > The Basics > Using Objectives: Map Coloring with Minimum Colors > Describe |
Describe |
INDEX
 PREVIOUS
NEXT
PREVIOUS
NEXT
|
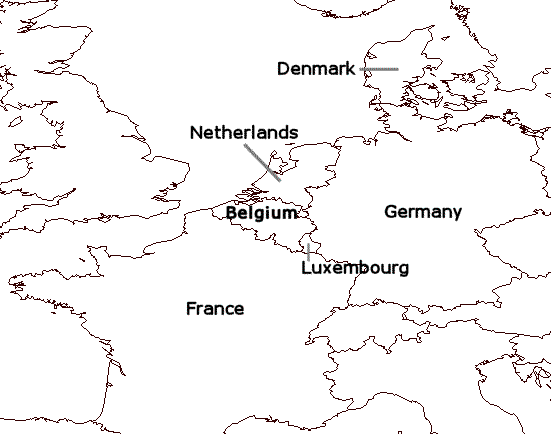
You will model and solve a map coloring problem similar to the one that you worked on in Chapter 2, Modeling and Solving a Simple Problem: Map Coloring. As you remember, that problem involves choosing colors for the countries on a map in such a way that at most four colors (blue, white, yellow, green) are used, and no neighboring countries are the same color. In this lesson, you will find a solution for a map coloring problem with six countries: Belgium, Denmark, France, Germany, Luxembourg, and the Netherlands. However, in this lesson only three colors (blue, white, and yellow) can be used to color the map.
In this problem, three colors are not going to be enough to color the map in such a way that no neighboring countries are the same color. So, what is the best approach for dealing with this situation? One option is to select what countries will share a color. If you look at the map, you could guess that if you removed one country, for example Luxembourg, from the set of constraints that no neighboring countries are the same color, you might be able to find a solution using just three colors. This is known as relaxing constraints.
However, you might want to try to have Luxembourg be a different color from some its neighbors, even if it cannot be a different color from all its neighbors. Suppose that you would most like to have Germany and Luxembourg be different colors if possible, then Belgium and Luxembourg if possible, and then France and Luxembourg if possible. You can represent these wishes as an objective. The relative importance of different constraints can be expressed in an objective. You can also use an objective to select the most appropriate solution when a problem has more than one solution--if there is more than one set of values for the variables that satisfy the constraints of the problem.
Step 1 - | Describe the problem |
Write a natural language description of this problem. Answer these questions:
| © Copyright IBM Corp. 1987, 2009. Legal terms. | PREVIOUS NEXT |