Complete Program and Output
 PREVIOUS
NEXT
PREVIOUS
NEXT
| IBM ILOG Scheduler User's Manual > Integrated Applications > Representing Time-Varying Resource Capacity > Complete Program and Output |
Complete Program and Output |
INDEX
 PREVIOUS
NEXT
PREVIOUS
NEXT
|
You can see the entire program capvar.cpp here or view it online in the standard distribution.
#include <ilsched/iloscheduler.h>
ILOSTLBEGIN
#if defined(ILO_SDXLOUTPUT)
#include "sdxloutput.h"
#endif
IloInt NumberOfActivities = 10;
IloInt NumberOfDays = 20;
IloNum AvailableCapacities[] = {2, 5, 5, 5, 3, 3, 2, 1, 0, 5,
2, 4, 5, 3, 2, 1, 4, 2, 1, 3};
IloNum Durations[] = {2, 4, 5, 6, 8, 2, 1, 3, 4, 6};
IloNum RequiredCapacities[] = {1, 1, 1, 1, 1, 2, 2, 1, 2, 1};
///////////////////////////////////////////////////////////////////////////////
//
// PROBLEM DEFINITION
//
///////////////////////////////////////////////////////////////////////////////
IloModel
DefineProblem(IloEnv env,
IloInt numberOfDays,
IloNum* availableCapacities,
IloInt numberOfActivities,
IloNum* durations,
IloNum* requiredCapacities,
IloDiscreteResource& resource)
{
/* CREATE THE MODEL. */
IloModel model(env);
IloSchedulerEnv schedEnv(env);
schedEnv.setOrigin(0);
schedEnv.setHorizon(numberOfDays);
/* CREATE THE RESOURCE. */
IloNum capacity = 0;
IloInt day;
for (day = 0; day < numberOfDays; day++)
if (capacity < availableCapacities[day])
capacity = availableCapacities[day];
resource = IloDiscreteResource(env, capacity);
/* POST THE MAXIMAL CAPACITY CONSTRAINTS. */
for (day = 0; day < NumberOfDays; day++)
resource.setCapacityMax(day, day + 1, availableCapacities[day]);
/* CREATE THE ACTIVITIES AND POST THE RESOURCE REQUIREMENT
CONSTRAINTS. */
char buffer[128];
IloInt i;
for (i = 0; i < numberOfActivities; i++) {
IloActivity activity(env, durations[i]);
sprintf(buffer, "A%ld", i);
activity.setName(buffer);
model.add(activity.requires(resource, requiredCapacities[i]));
}
/* RETURN THE MODEL. */
return model;
}
///////////////////////////////////////////////////////////////////////////////
//
// PRINTING OF SOLUTIONS
//
///////////////////////////////////////////////////////////////////////////////
void
PrintSolution(IloSolver solver, IloDiscreteResource resource)
{
IlcScheduler scheduler(solver);
IlcDiscreteResource schedResource =
scheduler.getDiscreteResource(resource);
for(IlcResourceConstraintIterator iterator(schedResource);
iterator.ok();
++iterator) {
IlcActivity activity = iterator.getActivity();
IlcCapRct capRct(*iterator);
solver.out() << " Activity " << activity.getName() << " requires "
<< capRct.getCapacity() << " person(s) from day "
<< activity.getStartMin() << " to day "
<< activity.getEndMin() << endl;
}
IlcInt timeMin = scheduler.getTimeMin();
IlcInt timeMax = scheduler.getTimeMax();
for (IlcInt day = timeMin; day < timeMax; day++)
solver.out() << " Work on day " << day << " requires "
<< schedResource.getCapacityMin(day) << " out of "
<< AvailableCapacities[day] << " person(s)" << endl;
}
///////////////////////////////////////////////////////////////////////////////
//
// MAIN FUNCTION
//
///////////////////////////////////////////////////////////////////////////////
int main()
{
try {
IloEnv env;
IloDiscreteResource resource;
IloModel model = DefineProblem(env,
NumberOfDays,
AvailableCapacities,
NumberOfActivities,
Durations,
RequiredCapacities,
resource);
IloSolver solver(model);
/* FILL AN ARRAY WITH THE VARIABLES REPRESENTING THE START TIMES
OF THE ACTIVITIES. */
IloNumVarArray startTimes(env, NumberOfActivities, 0, IloInfinity, ILOINT);
IloInt i = 0;
for (IloIterator<IloActivity> iterator(env);
iterator.ok();
++iterator) {
IloActivity activity = *iterator;
model.add(startTimes[i] == activity.getStartExpr());
i++;
}
/* DEFINE A GOAL THAT GENERATE A SOLUTION TO THE PROBLEM. */
IloGoal goal = IloGenerate(env, startTimes, IlcChooseMinMinInt);
if (solver.solve(goal)) {
PrintSolution(solver, resource);
solver.printInformation();
#if defined(ILO_SDXLOUTPUT)
IloSDXLOutput output(env);
ofstream outFile("capvar.xml");
output.write(IlcScheduler(solver), outFile);
outFile.close();
#endif
} else
solver.out() << "No solution!" << endl;
env.end();
} catch (IloException& exc) {
cout << exc << endl;
}
return 0;
}
///////////////////////////////////////////////////////////////////////////////
//
// RESULTS
//
///////////////////////////////////////////////////////////////////////////////
/*
Activity A9 requires 1 person(s) from day 2 to day 8
Activity A8 requires 2 person(s) from day 9 to day 13
Activity A7 requires 1 person(s) from day 1 to day 4
Activity A6 requires 2 person(s) from day 9 to day 10
Activity A5 requires 2 person(s) from day 12 to day 14
Activity A4 requires 1 person(s) from day 11 to day 19
Activity A3 requires 1 person(s) from day 1 to day 7
Activity A2 requires 1 person(s) from day 1 to day 6
Activity A1 requires 1 person(s) from day 0 to day 4
Activity A0 requires 1 person(s) from day 0 to day 2
Work on day 0 requires 2 out of 2 person(s)
Work on day 1 requires 5 out of 5 person(s)
Work on day 2 requires 5 out of 5 person(s)
Work on day 3 requires 5 out of 5 person(s)
Work on day 4 requires 3 out of 3 person(s)
Work on day 5 requires 3 out of 3 person(s)
Work on day 6 requires 2 out of 2 person(s)
Work on day 7 requires 1 out of 1 person(s)
Work on day 8 requires 0 out of 0 person(s)
Work on day 9 requires 4 out of 5 person(s)
Work on day 10 requires 2 out of 2 person(s)
Work on day 11 requires 3 out of 4 person(s)
Work on day 12 requires 5 out of 5 person(s)
Work on day 13 requires 3 out of 3 person(s)
Work on day 14 requires 1 out of 2 person(s)
Work on day 15 requires 1 out of 1 person(s)
Work on day 16 requires 1 out of 4 person(s)
Work on day 17 requires 1 out of 2 person(s)
Work on day 18 requires 1 out of 1 person(s)
Work on day 19 requires 0 out of 3 person(s)
*/
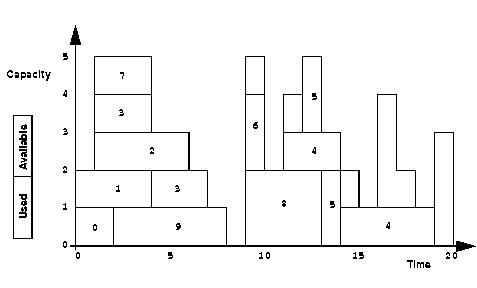
Figure 35.2 displays the solution. The gray areas indicate the capacity used in the solution, and the white areas indicate unused capacity.
| © Copyright IBM Corp. 1987, 2009. Legal terms. | PREVIOUS NEXT |