Complete Program and Output
 PREVIOUS
NEXT
PREVIOUS
NEXT
| IBM ILOG Scheduler User's Manual > Integrated Applications > Scheduling with State Resources: the Trolley Problem, with Transition Times > Complete Program and Output |
Complete Program and Output |
INDEX
 PREVIOUS
NEXT
PREVIOUS
NEXT
|
You can see the entire program trolley2.cpp here or view it online in the standard distribution.
#include <ilsched/iloscheduler.h>
ILOSTLBEGIN
const IloInt MACH1 = 1; // Machine 1 area
const IloInt MACH2 = 2; // Machine 2 area
const IloInt MACH3 = 3; // Machine 3 area
const IloInt AREAA = 4; // Arrival area
const IloInt AREAS = 5; // Stock area
const IloNum loadDuration = 20;
const IloInt numberOfJobs = 6;
const char* JobNames [] = { "J1", "J2", "J3", "J4", "J5", "J6"};
IloInt Machines1 [] = { 1, 2, 2, 1, 3, 2 };
IloNum Durations1 [] = { 80, 120, 80, 160, 180, 140 };
IloInt Machines2 [] = { 2, 3, 1, 3, 2, 3 };
IloNum Durations2 [] = { 60, 80, 60, 100, 80, 60 };
// M1 M2 M3 A S
IloNum TransitDurations[] = { 0, 50, 60, 50, 90, // M1
50, 0, 60, 90, 50, // M2
60, 60, 0, 80, 80, // M3
50, 90, 80, 0, 120, // A
90, 50, 80, 120, 0 };// S
IloNum getMaxTransitDuration(IloInt nbArea, IloNum* transitDurations){
IloNum max = 0;
IloInt size = nbArea*nbArea;
for (IloInt i = 0; i < size; i++)
if (transitDurations[i] > max) max = transitDurations[i];
return max;
}
///////////////////////////////////////////////////////////////////////////////
//
// DEFINITION OF THE JOB CLASS
//
///////////////////////////////////////////////////////////////////////////////
class Job {
public:
const char* _name;
IloActivity _loadA;
IloActivity _unload1;
IloActivity _process1;
IloActivity _load1;
IloActivity _unload2;
IloActivity _process2;
IloActivity _load2;
IloActivity _unloadS;
IloInt _area1;
IloInt _area2;
IloUnaryResource _machine1;
IloUnaryResource _machine2;
public:
Job(IloEnv env,
const char*,
IloNum loadDuration,
IloUnaryResource machine1, IloNum duration1, IloInt area1,
IloUnaryResource machine2, IloNum duration2, IloInt area2);
void addToModel(IloModel model,
IloStateResource trolley,
IloNumVar makespan,
IloTransitionParam transitionParam);
~Job();
void printSolution(IlcScheduler scheduler, ILOSTD(ostream)& out);
const char* getName() const { return _name;}
IloActivity getLoadA() const { return _loadA;}
IloActivity getUnload1() const { return _unload1;}
IloActivity getProcess1() const { return _process1;}
IloActivity getLoad1() const { return _load1;}
IloActivity getUnload2() const { return _unload2;}
IloActivity getProcess2() const { return _process2;}
IloActivity getLoad2() const { return _load2;}
IloActivity getUnloadS() const { return _unloadS;}
};
Job::Job(IloEnv env,
const char* name,
IloNum loadDuration,
IloUnaryResource machine1, IloNum duration1, IloInt area1,
IloUnaryResource machine2, IloNum duration2, IloInt area2)
: _name(name),
_loadA( env,loadDuration),
_unload1( env,loadDuration),
_process1(env,duration1),
_load1( env,loadDuration),
_unload2( env,loadDuration),
_process2(env,duration2),
_load2( env,loadDuration),
_unloadS( env,loadDuration),
_area1(area1),
_area2(area2),
_machine1(machine1),
_machine2(machine2)
{
char buffer[256];
sprintf(buffer, "arrival_load_%s", name);
_loadA.setName(buffer);
sprintf(buffer, "area%ld_unload_%s", area1, name);
_unload1.setName(buffer);
sprintf(buffer, "machine%ld_%s", area1, name);
_process1.setName(buffer);
sprintf(buffer, "area%ld_load_%s", area1, name);
_load1.setName(buffer);
sprintf(buffer, "area%ld_unload_%s", area2, name);
_unload2.setName(buffer);
sprintf(buffer, "machine%ld_%s", area2, name);
_process2.setName(buffer);
sprintf(buffer, "area%ld_load_%s", area2, name);
_load2.setName(buffer);
sprintf(buffer, "stock_load_%s", name);
_unloadS.setName(buffer);
_loadA.setTransitionType(AREAA - 1);
_unload1.setTransitionType(_area1 - 1);
_load1.setTransitionType(_area1 - 1);
_unload2.setTransitionType(_area2 - 1);
_load2.setTransitionType(_area2 - 1);
_unloadS.setTransitionType(AREAS - 1);
}
Job::~Job()
{}
void Job::addToModel(IloModel model,
IloStateResource trolley,
IloNumVar makespan,
IloTransitionParam transitionParam)
{
/* ADD MACHINE REQUIREMENT CONSTRAINTS */
model.add(_process1.requires(_machine1));
model.add(_process2.requires(_machine2));
/* ADD TEMPORAL CONSTRAINTS BETWEEN ACTIVITIES */
IloNum delay = transitionParam.getValue((IloInt)_loadA.getTransitionType(),
(IloInt)_unload1.getTransitionType());
model.add(_unload1.startsAfterEnd(_loadA, delay));
model.add(_process1.startsAfterEnd(_unload1));
model.add(_load1.startsAfterEnd(_process1));
delay = transitionParam.getValue((IloInt)_load1.getTransitionType(),
(IloInt)_unload2.getTransitionType());
model.add(_unload2.startsAfterEnd(_load1, delay));
model.add(_process2.startsAfterEnd(_unload2));
model.add(_load2.startsAfterEnd(_process2));
delay = transitionParam.getValue((IloInt)_load2.getTransitionType(),
(IloInt)_unloadS.getTransitionType());
model.add(_unloadS.startsAfterEnd(_load2, delay));
/* ADD TROLLEY POSITION REQUIREMENTS */
model.add(_loadA.requires(trolley, (IloAny)AREAA));
model.add(_unload1.requires(trolley, (IloAny)_area1));
model.add(_load1.requires(trolley, (IloAny)_area1));
model.add(_unload2.requires(trolley, (IloAny)_area2));
model.add(_load2.requires(trolley, (IloAny)_area2));
model.add(_unloadS.requires(trolley, (IloAny)AREAS));
/* ADD MAKESPAN CONSTRAINT */
model.add(_unloadS.endsBefore(makespan));
}
void Job::printSolution(IlcScheduler scheduler, ILOSTD(ostream)& out)
{
/* PRINT JOB */
out
<< "JOB " << _name << endl
<< "\t Load at area A: "
<< scheduler.getActivity( _loadA ) << endl
<< "\t Unload at area " << (long)_area1 << ": "
<< scheduler.getActivity( _unload1 ) << endl
<< "\t Process on machine " << (long)_area1 << ": "
<< scheduler.getActivity( _process1 ) << endl
<< "\t Load at area " << (long)_area1 << ": "
<< scheduler.getActivity( _load1 ) << endl
<< "\t Unload at area " << (long)_area2 << ": "
<< scheduler.getActivity( _unload2 ) << endl
<< "\t Process on machine " << (long)_area2 << ": "
<< scheduler.getActivity( _process2 ) << endl
<< "\t Load at area " << (long)_area2 << " : "
<< scheduler.getActivity( _load2 ) << endl
<< "\t Unload at area S: "
<< scheduler.getActivity( _unloadS ) << endl;
}
///////////////////////////////////////////////////////////////////////////////
//
// PROBLEM DEFINITION
//
///////////////////////////////////////////////////////////////////////////////
#if defined(ILO_SDXLOUTPUT)
#include "sdxltrolley.h"
#endif
IloModel DefineModel(IloEnv env,
const char** jobNames,
IloNum* transitDurations,
IloInt* machines1,
IloNum* durations1,
IloInt* machines2,
IloNum* durations2,
IloAnyArray& jobs,
IloStateResource& trolley,
IloArray<IloUnaryResource>& machines,
IloNumVar& makespan)
{
IloInt i, j;
IloModel model(env);
/* CREATE THE MAKESPAN VARIABLE. */
IloNum horizon =
numberOfJobs * ((6 * loadDuration) +
(4 * getMaxTransitDuration(5, transitDurations)));
for (i = 0; i < numberOfJobs; i++)
horizon += durations1[i] + durations2[i];
makespan = IloNumVar(env,0,horizon,ILOINT);
/* CREATE THE TROLLEY POSITION RESOURCE */
IloAnyArray arrayOfPossibleAreas(env,
5,
(IloAny)AREAA,
(IloAny)MACH1,
(IloAny)MACH2,
(IloAny)MACH3,
(IloAny)AREAS);
IloAnySet setOfPossibleAreas(env,arrayOfPossibleAreas);
trolley = IloStateResource(env,setOfPossibleAreas, "trolley");
/* CREATE THE (SYMMETRIC) TRANSITION TIME TABLE */
IloTransitionParam transitionParam(env, 5, IloTrue);
for (i = 0; i < 5; i++)
for (j = i; j < 5; j++)
transitionParam.setValue(i,j,transitDurations[j + (5 * i)]);
/* ASSOCIATE A TRANSITION TIME TO THE RESOURCE */
IloTransitionTime transitionTime(trolley,transitionParam);
/* SELECT APPROPRIATE ENFORCEMENT LEVEL */
trolley.setTransitionTimeEnforcement(IloBasic);
trolley.setCapacityEnforcement(IloMediumHigh);
/* CREATE THE MACHINES RESOURCES */
char buffer[256];
machines = IloArray<IloUnaryResource>(env, 3);
for (i = 0; i < 3; i++) {
sprintf(buffer, "machine%ld", i + 1);
machines[i] = IloUnaryResource(env, buffer);
}
/* CREATION OF JOB INSTANCES */
jobs = IloAnyArray(env, numberOfJobs);
for (i = 0; i < numberOfJobs; i++) {
Job* job = new (env) Job(env,
jobNames[i],
loadDuration,
machines[machines1[i] - 1],
durations1[i], machines1[i],
machines[machines2[i] - 1],
durations2[i], machines2[i]);
jobs[i] = job;
job->addToModel(model, trolley, makespan, transitionParam);
}
/* WE LOOK FOR AN OPTIMAL SOLUTION */
model.add(IloMinimize(env, makespan));
/* RETURN THE CREATED MODEL */
return model;
}
///////////////////////////////////////////////////////////////////////////////
//
// PRINTING OF SOLUTIONS
//
///////////////////////////////////////////////////////////////////////////////
void PrintSolution(IloSolver solver,
IloAnyArray jobs,
IloStateResource trolley,
IloArray<IloUnaryResource> machines,
IloNumVar makespan)
{
IlcScheduler scheduler(solver);
solver.out() << "makespan = " << solver.getMin(makespan) << endl;
for (IloInt i = 0; i < numberOfJobs; i++)
((Job*) jobs[i])->printSolution(scheduler, solver.out());
solver.out() << "TROLLEY POSITIONS: " << endl;
IlcStateResourceIterator ite(scheduler);
IlcAnyTimetable tt = scheduler.getStateResource(trolley).getTimetable();
for (IlcAnyTimetableCursor cr(tt,0); cr.ok(); ++cr)
if (cr.isBound())
solver.out() << "\t [" << cr.getTimeMin()
<< "," << cr.getTimeMax()
<< "): Position " << (long)cr.getValue()
<< endl;
solver.printInformation();
#if defined(ILO_SDXLOUTPUT)
IloSDXLTrolleyOutput output(solver.getEnv());
ofstream outFile("trolley2.xml");
output.writeTrolley(scheduler,
outFile,
jobs,
trolley,
(IloInt) 1000,
machines,
makespan);
outFile.close();
#endif
}
///////////////////////////////////////////////////////////////////////////////
//
// MAIN FUNCTION
//
///////////////////////////////////////////////////////////////////////////////
int main(int argc, char** argv) {
IloInt failLimit = 1000;
if (argc > 1)
failLimit = atol(argv[1]);
try {
IloEnv env;
IloAnyArray jobs;
IloStateResource trolley;
IloArray<IloUnaryResource> machines;
IloNumVar makespan;
IloModel model = DefineModel(env,
JobNames,
TransitDurations,
Machines1, Durations1,
Machines2, Durations2,
jobs,
trolley,
machines,
makespan);
IloBool solved = IloFalse;
IloNum minMakespan = 0.;
IloSolver solver(model);
IloGoal unlimitedGoal = IloSetTimesForward(env, makespan);
IloGoal limitedGoal = IloLimitSearch(env, unlimitedGoal,
IloFailLimit(env,failLimit) );
solver.startNewSearch(limitedGoal);
while (solver.next()==IlcTrue) {
solved = IloTrue;
minMakespan = solver.getMin(makespan);
solver.out() << "SOLUTION WITH MAKESPAN "
<< minMakespan << endl;
}
solver.endSearch();
if (solved){
makespan.setBounds(minMakespan,minMakespan);
solver.solve(unlimitedGoal);
PrintSolution(solver,jobs,trolley,machines,makespan);
} else {
solver.out() << "NO SOLUTION FOUND" << endl;
}
env.end();
} catch (IloException& exc) {
cout << exc << endl;
}
return 0;
}
///////////////////////////////////////////////////////////////////////////////
//
// RESULTS
//
///////////////////////////////////////////////////////////////////////////////
/*
SOLUTION WITH MAKESPAN 1220
SOLUTION WITH MAKESPAN 1130
SOLUTION WITH MAKESPAN 1110
SOLUTION WITH MAKESPAN 1070
SOLUTION WITH MAKESPAN 990
SOLUTION WITH MAKESPAN 980
makespan = 980
JOB J1
Load at area A: [0 -- 20 --> 20]
Unload at area 1: [70 -- 20 --> 90]
Process on machine 1: [250 -- 80 --> 330]
Load at area 1: [330 -- 20 --> 350]
Unload at area 2: [400 -- 20 --> 420]
Process on machine 2: [500 -- 60 --> 560]
Load at area 2 : [580 -- 20 --> 600]
Unload at area S: [960 -- 20 --> 980]
JOB J2
Load at area A: [0 -- 20 --> 20]
Unload at area 2: [140 -- 20 --> 160]
Process on machine 2: [160 -- 120 --> 280]
Load at area 2: [400 -- 20 --> 420]
Unload at area 3: [500 -- 20 --> 520]
Process on machine 3: [680 -- 80 --> 760]
Load at area 3 : [810 -- 20 --> 830]
Unload at area S: [960 -- 20 --> 980]
JOB J3
Load at area A: [0 -- 20 --> 20]
Unload at area 2: [140 -- 20 --> 160]
Process on machine 2: [420 -- 80 --> 500]
Load at area 2: [580 -- 20 --> 600]
Unload at area 1: [650 -- 20 --> 670]
Process on machine 1: [670 -- 60 --> 730]
Load at area 1 : [730 -- 20 --> 750]
Unload at area S: [960 -- 20 --> 980]
JOB J4
Load at area A: [0 -- 20 --> 20]
Unload at area 1: [70 -- 20 --> 90]
Process on machine 1: [90 -- 160 --> 250]
Load at area 1: [300 -- 20 --> 320]
Unload at area 3: [500 -- 20 --> 520]
Process on machine 3: [580 -- 100 --> 680]
Load at area 3 : [810 -- 20 --> 830]
Unload at area S: [960 -- 20 --> 980]
JOB J5
Load at area A: [0 -- 20 --> 20]
Unload at area 3: [220 -- 20 --> 240]
Process on machine 3: [240 -- 180 --> 420]
Load at area 3: [500 -- 20 --> 520]
Unload at area 2: [580 -- 20 --> 600]
Process on machine 2: [600 -- 80 --> 680]
Load at area 2 : [890 -- 20 --> 910]
Unload at area S: [960 -- 20 --> 980]
JOB J6
Load at area A: [0 -- 20 --> 20]
Unload at area 2: [140 -- 20 --> 160]
Process on machine 2: [280 -- 140 --> 420]
Load at area 2: [420 -- 20 --> 440]
Unload at area 3: [500 -- 20 --> 520]
Process on machine 3: [520 -- 60 --> 580]
Load at area 3 : [810 -- 20 --> 830]
Unload at area S: [960 -- 20 --> 980]
TROLLEY POSITIONS:
[0,20): Position 4
[70,90): Position 1
[140,160): Position 2
[220,240): Position 3
[300,320): Position 1
[330,350): Position 1
[400,440): Position 2
[500,520): Position 3
[580,600): Position 2
[650,670): Position 1
[730,750): Position 1
[810,830): Position 3
[890,910): Position 2
[960,980): Position 5
*/
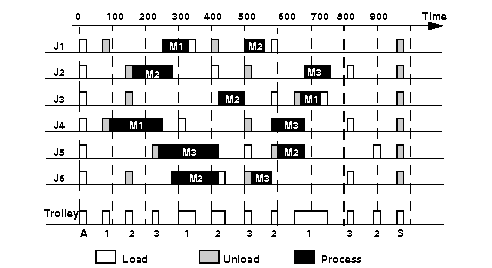
This solution corresponds to a maximal number of fails per optimization step of 1000. It is represented in Figure 33.2. (Positions 4 and 5 in the output results correspond to the areas A and S in the diagram.)
Notice the effect of transition times on the bottom line of the schedule, representing the trolley. In the first version of the example, the trolley moved from one area to another 19 times. When transition times are taken into account, moves become critical with respect to the makespan criterion: which explains why the trolley performs only 11 moves in the solution shown in Figure 33.2.
| © Copyright IBM Corp. 1987, 2009. Legal terms. | PREVIOUS NEXT |