The problem described in this chapter consists of n jobs to be performed in a shop equipped with m machines. A job corresponds to the processing of an item. Each item needs to be sequentially processed on k specified machines with known processing times.

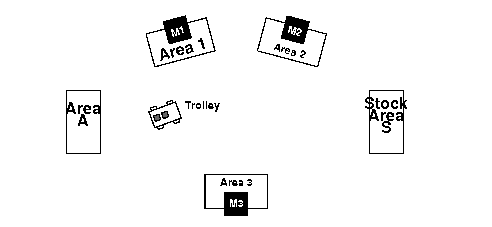
In the problem, we want to model the physical distance between machines. The items to be processed are initially available in area A of the shop. Each time an item must be processed on a machine M, it must be brought to the area of this machine with a trolley. After the item has been processed, it must be stocked in area S of the shop.

Moving an item from an area x to an area y means (1) loading the item on the trolley at area x, (2) moving the trolley from area x to area y and, finally, (3) unloading the item at area y. We suppose that the activities of loading (and unloading) items can overlap, assuming that the trolley is in the same area as the items. We search for a solution that minimizes the makespan of the schedule.

The following C++ arrays provide the data defining the problem. The ith column of arrays JobNames, Machines1, Durations1, Machines2 and Durations2 respectively define: the name of the ith job, the number j of its first machine Mj, the processing time on this machine, the number k of its second machine Mk, and the processing time on this machine.

Two additional parameters are defined: the duration of loading (and unloading) activities and the number of jobs in the problem.

const IloNum loadDuration = 20;
const IloInt numberOfJobs = 6;

const char*  JobNames [] = { "J1",   "J2",   "J3",   "J4",   "J5",   "J6"};
IloInt Machines1      [] = { 1,      2,      2,      1,      3,      2   };
IloNum Durations1     [] = { 80,     120,    80,     160,    180,    140 };
IloInt Machines2      [] = { 2,      3,      1,      3,      2,      3   };
IloNum Durations2     [] = { 60,     80,     60,     100,    80,     60  };