Complete Program and Output--Example 7
 PREVIOUS
NEXT
PREVIOUS
NEXT
| IBM ILOG Scheduler User's Manual > Getting Started with Scheduler > Adding Integral and Functional Constraints > Complete Program and Output--Example 7 |
Complete Program and Output--Example 7 |
INDEX
 PREVIOUS
NEXT
PREVIOUS
NEXT
|
You can see the entire program gsEff.cpp here or view it online in the standard distribution.
#include <ilsched/iloscheduler.h>
ILOSTLBEGIN
///////////////////////////////////////////////////////////////////////////////
//
// PROBLEM DEFINITION
//
///////////////////////////////////////////////////////////////////////////////
const IloNum dur[] = { 7, 3, 8, 3, 1, 2, 1, 2, 1, 1};
const IloInt NumberOfActivities = 10;
const IloNum horizon = 10*7; /* MAXIMAL SCHEDULE OF TEN WEEKS */
const IloNum maxBudget = 50000;
const IloNum maxMakespan = 50;
IloModel DefineModel(IloEnv env,
IloNum MaxMakespan,
IloNumVar &totalCost,
IloNumVarArray& costs,
IloSchedulerSolution solution)
{
IloModel model(env);
IloSchedulerEnv schedEnv(env);
schedEnv.getBreakListParam().keepOpen();
schedEnv.setHorizon(horizon);
/* CREATE THE ACTIVITIES. */
IloActivity activities[NumberOfActivities];
IloActivity masonry(env, dur[0], "masonry ");
IloActivity carpentry(env, dur[1], "carpentry ");
IloActivity plumbing(env, dur[2], "plumbing ");
IloActivity ceiling(env, dur[3], "ceiling ");
IloActivity roofing(env, dur[4], "roofing ");
IloActivity painting(env, dur[5], "painting ");
IloActivity windows(env, dur[6], "windows ");
IloActivity facade(env, dur[7], "facade ");
IloActivity garden(env, dur[8], "garden ");
IloActivity moving(env, dur[9], "moving ");
/* STORE THE ACTIVITIES */
activities[0] = masonry;
activities[1] = carpentry;
activities[2] = plumbing;
activities[3] = ceiling;
activities[4] = roofing;
activities[5] = painting;
activities[6] = windows;
activities[7] = facade;
activities[8] = garden;
activities[9] = moving;
/* ADD THE TEMPORAL CONSTRAINTS. */
model.add(carpentry.startsAfterEnd(masonry));
model.add(plumbing.startsAfterEnd(masonry));
model.add(ceiling.startsAfterEnd(masonry));
model.add(roofing.startsAfterEnd(carpentry));
model.add(painting.startsAfterEnd(ceiling));
model.add(windows.startsAfterEnd(roofing));
model.add(facade.startsAfterEnd(roofing));
model.add(facade.startsAfterEnd(plumbing));
model.add(garden.startsAfterEnd(roofing));
model.add(garden.startsAfterEnd(plumbing));
model.add(moving.startsAfterEnd(windows));
model.add(moving.startsAfterEnd(facade));
model.add(moving.startsAfterEnd(garden));
model.add(moving.startsAfterEnd(painting));
model.add( moving.endsBefore(MaxMakespan) );
/* CREATE THE WORKER RESOURCE. */
IloUnaryResource worker(env);
#ifndef NO_CALENDAR
worker.ignoreCalendarConstraints();
#endif // NO_CALENDAR
/* MODEL WORKER'S EFFICIENCY */
IloNum day;
IloGranularFunction efficiency(env, 0, horizon, 100);
for(day=0; day+7<=horizon; day+=7) {
efficiency.setValue(day+2, day+3, 50); // part-time wednesday
efficiency.setValue(day+5, day+6, 50); // saturdays
efficiency.setValue(day+6, day+7, 0); // sundays
}
efficiency.setValue( 8, 9, 0); // Tuesday of week #2 is a day off
efficiency.setValue(14,15, 0); // Monday of week #3 is a day off
model.add( IloResourceIntegralConstraint(worker,
IloProcessingTimeVariable,
efficiency));
/* CREATE COST CURVE */
IloNum dailyCost = 0;
IloNum overallCost = 0;
IloGranularFunction costFunction(env, 0, horizon);
for(day=0; day<horizon; day+=1) {
costFunction.setValue(day, day+1, overallCost);
if (day<3) dailyCost = 1000.0;
else if (day<7) dailyCost = 900.0;
else dailyCost = 700.0;
overallCost += dailyCost;
}
model.add( IloResourceFunctionalConstraint(worker,
IloExternalVariable,
costFunction,
IloDurationVariable) );
costs = IloNumVarArray(env);
for(IloInt i=0; i<NumberOfActivities; ++i)
{
/* SET ACTIVITY AS BREAKABLE */
activities[i].setBreakable(IloTrue);
/* ADD THE WORKER RESOURCE CONSTRAINTS. */
model.add( activities[i].requires(worker) );
/* CREATE THE INDIVIDUAL COST VARIABLE */
IloNumVar cost(env, 1, maxBudget, ILOINT);
costs.add( cost );
activities[i].setExternalVariable( cost );
solution.getSolution().add(cost);
/* REGISTER ACTIVITIES TO BE STORED IN THE SOLUTION */
solution.add( activities[i] );
}
/* SET THE OBJECTIVE: MINIMIZE THE TOTAL COST VARIABLE */
totalCost = IloNumVar(env, 0, maxBudget, ILOINT);
model.add( totalCost == IloSum(costs) );
model.add( IloMinimize(env, totalCost) );
/* REGISTER VARIABLES TO BE STORED IN THE SOLUTION */
solution.getSolution().add(totalCost);
return model;
}
///////////////////////////////////////////////////////////////////////////////
//
// PRINTING OF SOLUTIONS
//
///////////////////////////////////////////////////////////////////////////////
void PrintSolution(const IloSolver& solver,
const IloSchedulerSolution solution,
const IloNumVar totalCost,
IloNum MaxMakespan)
{
solver.out() << "Solution with cost "
<< solution.getSolution().getMin(totalCost)
<< " and maximum makespan " << MaxMakespan
<< endl << endl;
for (IloSchedulerSolution::ActivityIterator iter(solution);
iter.ok(); ++iter)
{
IloActivity act = *iter;
solver.out() << act.getName();
solver.out() << " [" << solution.getStartMin(act);
solver.out() << " -- " << solution.getProcessingTimeMin(act);
solver.out() << " (d=" << solution.getDurationMin(act);
solver.out() << ") --> " << solution.getEndMin(act);
solver.out() << " ] cost:" << solution.getExternalVariableMin(act);
solver.out() << endl;
}
solver.out() << endl;
}
///////////////////////////////////////////////////////////////////////////////
//
// MAIN FUNCTION
//
///////////////////////////////////////////////////////////////////////////////
int main()
{
try {
IloEnv env;
IloNumVar totalCost;
IloNumVarArray costs;
IloSchedulerSolution solution(env);
IloModel model = DefineModel(env, maxMakespan, totalCost, costs, solution);
IloSolver solver(model);
IloGoal goal = IloGenerate(env, costs) &&
IloSetTimesForward(env);
if (solver.solve(goal)) {
solution.store( IlcScheduler(solver) );
PrintSolution(solver, solution, totalCost, maxMakespan);
}
else
solver.out() << "No Solution." << endl;
solution.end();
env.end();
} catch (IloException& exc) {
cout << exc << endl;
}
return 0;
}
///////////////////////////////////////////////////////////////////////////////
//
// RESULTS
//
///////////////////////////////////////////////////////////////////////////////
/*
Solution with cost 34600 and maximum makespan 50
masonry [0 -- 7 (d=11) --> 11 ] cost:9400
carpentry [21 -- 3 (d=4) --> 25 ] cost:3900
plumbing [30 -- 8 (d=11) --> 41 ] cost:9400
ceiling [15 -- 3 (d=4) --> 19 ] cost:3900
roofing [25 -- 1 (d=1) --> 26 ] cost:1000
painting [28 -- 2 (d=2) --> 30 ] cost:2000
windows [43 -- 1 (d=1) --> 44 ] cost:1000
facade [45 -- 2 (d=2) --> 47 ] cost:2000
garden [42 -- 1 (d=1) --> 43 ] cost:1000
moving [49 -- 1 (d=1) --> 50 ] cost:1000
*/
Figure 7.1 displays the solution to our problem.
One sees that there is not much slack to finish the house earlier with the selected sequence.
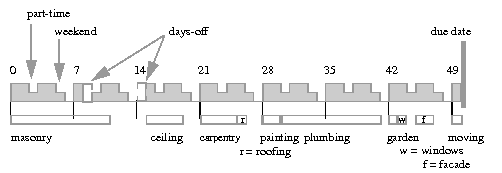
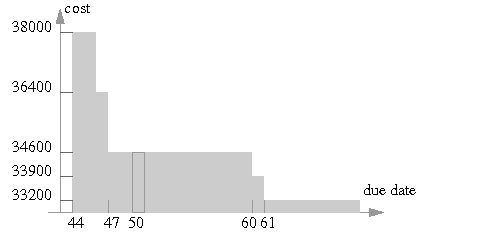
Having a due date of 50 days has an impact on the total cost. The long activities (masonry and plumbing) are best not executed across weekends or days-off. However, with a due date of 50 days, there is not enough time to delay these long activities until more convenient time-slots are available. Increasing the due date leaves more slack time to avoid processing long activities during days off, thus reducing the total cost. Figure 7.2 shows the optimal cost found for various due dates ranging from 44 to 70 days. The figure shows that it is possible to finish in 47 days at the same cost of finishing in 50 days. With a due date tighter than 47 days, the cost increases fast as some activities are executed over weekends. Finishing before 44 days is impossible.
| © Copyright IBM Corp. 1987, 2009. Legal terms. | PREVIOUS NEXT |