You can see the entire program balpos.cpp here or view it in the standard distribution.

#include <ilsched/iloscheduler.h>
 
ILOSTLBEGIN
 
IloInt NumberOfActivities = 15;
 
//---------------------------- PROBLEM 1 ------------------------------------
IloInt Durations01 [] = { 
  5, 5, 5, 5, 5, 7, 7, 8, 8, 9, 14, 14, 14, 14, 15 };
 
IloInt NumberOfConstraints01 = 7;
 
IloInt Constraints01 [] = {
  14, 15, 5,
  4,  6,  24, 
  0,  3,  38,
  1,  11, 117,
  1,  8,  83,
  4,  8,  50,
  8,  14, 59 };
 
//---------------------------- PROBLEM 2 ------------------------------------
IloInt Durations02 [] = { 
  5, 7, 7, 8, 8, 8, 8, 10, 10, 10, 11, 11, 13, 14, 15 };
 
IloInt NumberOfConstraints02 = 7;
 
IloInt Constraints02 [] = {
  3, 11, 88,
  6, 8,  27,
  1, 6,  48,
  5, 8,  38,
  9, 15, 55,
  1, 3,  17,
  1, 4,  27 };
 
//---------------------------- PROBLEM 3 ------------------------------------
IloInt Durations03 [] = { 
  5, 6, 6, 7, 7, 7, 8, 9, 9, 9, 10, 11, 14, 14, 15 };
 
IloInt NumberOfConstraints03 = 7;
 
IloInt Constraints03 [] = {
  2, 3, 15,
  5, 7, 17,
  1, 7, 71,
  2, 5, 44,
  2, 6, 49,
  2, 4, 29,
  0, 3, 34 };
 
 
//----------------------- COMPUTE MAX MAKESPAN ----------------------------
IloNum getMakespanMax(const IloEnv& env,
                      IloInt numberOfActivities,
                      IloInt numberOfConstraints,
                      IloInt* durations,
                      IloInt* constraints) {
  // THIS FUNCTION COMPUTES AN UPPER BOUND ON THE MAKESPAN BY ASSUMING
  // ALL THE ACTIVITIES HAVE A  DURATION EQUAL TO THE LONGEST ACTIVITY
  // OF THE   PROBLEM.
  IloModel model(env);
  
  IloNumVar makespan(env, 0, IloInfinity, ILOINT);
  IloInt i, j, k, t;
 
  // COMPUTE MAXIMAL DURATION OF ACTIVITIES
  IloInt dmax = 0;
  for (i=0; i < numberOfActivities; i++)
    if (durations[i] > dmax)
      dmax = durations[i];
 
  IloActivity lact; 
  IloNumExprArray times(env, numberOfActivities+1);
  for (i=0; i < numberOfActivities; i++) {
    // USE ACTIVITIES WITH MAXIMAL DURATION
    IloActivity act(env, dmax);
    times[i] = act.getStartExpr();
    if (i > 0)
      model.add(act.startsAfterEnd(lact));
    lact = act;
  }  
  model.add(lact.endsBefore(makespan));
  times[numberOfActivities] = makespan;
 
  // ADD MINIMAL DELAY CONSTRAINTS
  for (k=0; k < numberOfConstraints; k++) {
    i = constraints[3*k];
    j = constraints[(3*k) + 1];
    t = constraints[(3*k) + 2];
    model.add(times[j]-times[i] >= t);
  }
 
  // JUST PROPAGATE THE PERT
  IloSolver solver(model);
  IlcSearch s = solver.newSearch(IloGoalTrue(env));
  s.next();
  IloNum makespanMax = solver.getMin(makespan);
  solver.end();
 
  return makespanMax;
}
 
//----------------------------- MODEL -------------------------------------
IloModel
DefineModel(const IloEnv& env,
            IloInt numberOfActivities,
            IloInt numberOfConstraints,
            IloInt* durations,
            IloInt* constraints,
            IloNumVar& makespan)
{
  IloModel model(env);
  IloUnaryResource ures(env);
  // THIS ENFORCEMENT LEVEL WILL POST THE BALANCE CONSTRAINT
  ures.setCapacityEnforcement(IloExtended);
  // THIS ENFORCEMENT LEVEL WILL POST THE PRECEDENCE GRAPH CONSTRAINT
  ures.setPrecedenceEnforcement(IloExtended);
  IloReservoir reserv(env, 2, 0); 
  // THIS ENFORCEMENT LEVEL WILL POST THE BALANCE CONSTRAINT
  reserv.setCapacityEnforcement(IloExtended);
  // COMPUTES UPPER BOUND ON MAKESPAN
  IloNum makespanMax = getMakespanMax(env,
                                      numberOfActivities,
                                      numberOfConstraints,
                                      durations,
                                      constraints);
  makespan = IloNumVar(env, 0, makespanMax, ILOINT);
 
  IloNumExprArray times(env, numberOfActivities + 1);
  IloActivityArray acts(env, numberOfActivities);
  
  // COMPUTE DURATION OF SHORTEST ACTIVITY
  IloInt dmin = IloIntMax;
  IloInt i, j, k, t;
  for (i=0; i < numberOfActivities; i++)
    if (durations[i] < dmin)
      dmin = durations[i];
 
  IloActivity lprod;
  for (i=0; i < numberOfActivities; i++) {
    acts[i]= IloActivity(env, durations[i]);
    model.add(acts[i].requires(ures));
    model.add(acts[i].requires(reserv, 1, IloAfterEnd));
    model.add(acts[i].requires(reserv, 1, IloAfterStart));
    model.add(acts[i].endsBefore(makespan));
    IloActivity prod(env, 1);
    model.add(prod.provides(reserv, 2, IloAfterStart));
    times[i] = prod.getStartExpr();
    if (i > 0)
      // BUILD CHAIN OF PRODUCERS
      model.add(prod.startsAfterStart(lprod, dmin));
    lprod = prod;
  }  
  times[numberOfActivities] = makespan;
  model.add(times[numberOfActivities-1] + dmin <= makespan); 
 
  // BREAK EVIDENT SYMMETRIES BETWEEN ACTIVITIES WITH SAME DURATION
  for (i=0; i < numberOfActivities - 1; i++) 
    for (j=i+1; j < numberOfActivities; j++) 
      if (durations[i] == durations[j]) {
        model.add(acts[j].startsAfterEnd(acts[i]));
        break;
      }
 
  // ADD DELAY CONSTRAINTS
  for (k=0; k < numberOfConstraints; k++) {
    i = constraints[3*k];
    j = constraints[(3*k) + 1];
    t = constraints[(3*k) + 2];
    model.add(times[j]-times[i] >= t);
  }
 
  return model;
}
 
//-------------------------- DISPLAY SOLUTION -----------------------------
void
PrintSolution(const IloSolver& solver)
{
  IlcScheduler sched(solver);
  IlcUnaryResource res = *(IlcUnaryResourceIterator(sched));
  for(IlcResourceConstraintIterator ite(res); ite.ok(); ++ite)
    solver.out() << (*ite).getActivity() << endl;
}
 
//---------------------- INITIALIZE PARAMETERS -----------------------------
void
InitParameters(int argc,
               char** argv,
               IloInt& numberOfConstraints,
               IloInt*& durations,
               IloInt*& constraints)
{
  IloInt p = 1;
  if (argc > 1)
    p = atol(argv[1]);
  
  switch (p) {
  case (1):
    numberOfConstraints = NumberOfConstraints01;
    durations   = Durations01;
    constraints = Constraints01;
    break;
  case (2):
    numberOfConstraints = NumberOfConstraints02;
    durations   = Durations02;
    constraints = Constraints02;
    break;
  case (3):
    numberOfConstraints = NumberOfConstraints03;
    durations   = Durations03;
    constraints = Constraints03;
    break;
  }
}
 
//------------------------- SOLVE PROBLEM ----------------------------------
int main(int argc, char* argv[])
{ 
  try {
    IloEnv env;
    
    IloInt numberOfActivities = NumberOfActivities;
    IloInt numberOfConstraints;
    IloInt* durations;
    IloInt* constraints;
    
    InitParameters(argc, argv, 
                   numberOfConstraints, 
                   durations, constraints);
 
    IloNumVar makespan;
    IloModel model = DefineModel(env,
                                 numberOfActivities,
                                 numberOfConstraints,
                                 durations,
                                 constraints,
                                 makespan);
    
    model.add(IloMinimize(env, makespan));
    IloSolver solver(model);
    IlcSearch search = solver.newSearch(IloRankForward(env, makespan));
    
    IloInt sumd = 0;
    for (IloInt i=0; i < numberOfActivities; i++)
      sumd += durations[i];
    
    while (search.next()) {
      solver.out() << "SOLUTION WITH SLACK = " 
                   << solver.getIntVar(makespan).getMin() - sumd << endl;    
      PrintSolution(solver);
    }
    solver.printInformation();
    solver.end();
    env.end();
    
  } catch (IloException& exc) {
    cout << exc << endl;
  }
  return 0;
}
 

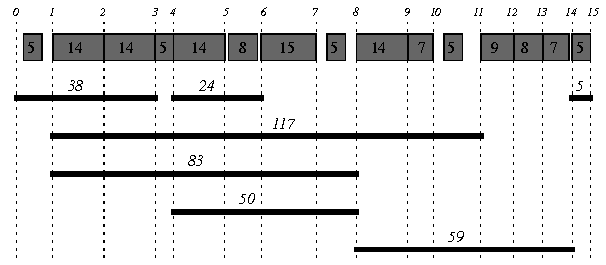
This optimal solution is quickly found after 2 iterations and 28 backtracks.