In terms of the specification of the problem, a multiple depot pickup and delivery problem is much the same as a standard single depot problem. The main difference is that not all vehicles are located at the same node. Multiple depot problems may also have some properties which are local to each depot, for instance opening hours, although such variations are not addressed here. The constraints here are the usual ones of vehicle capacity and time windows. The object is to minimize the total distance traveled.

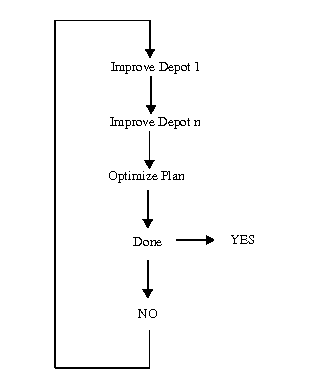
The MDPDP problem is broken down to a set of subproblems using Concert Technology: one subproblem per depot. Each subproblem is then improved independently. This has the advantage that the whole problem can be solved more quickly. However, there is a disadvantage. By decomposing the problem, the quality of solution obtained can be poorer than if the problem were considered as a whole. This problem, therefore, uses a mixed technique where each subproblem is improved independently and then the whole problem is improved. The process is then iterated with the subproblems being improved once more in light of the changes made while optimizing the whole problem. This process continues until some stopping condition is met. In this example, the stopping condition is that no more improvement takes place. This process is shown in the following figure:

To perform the decomposition of the problem into subproblems, one model, an instance of IloModel, per subproblem is maintained. Each of these models contains the dimensions of the problem and the vehicles particular to the depot in question. In addition, each such model contains constraints particular to the depot, such as the time constraints on vehicles based at that depot. A model of the whole problem, containing the depot models, is also maintained. The assignment of depots to visits is not known in advance, and, in fact, may change during the improvement process. It will thus be necessary to add visits to and remove visits from models. To ease this process, a small model is created for each visit which holds the visit along with constraints pertaining to the visit itself (for instance, time windows). In this way, visits, together with their pertinent constraints, can be transferred from model to model. A reference to this model is stored in the visit itself using IloVisit::setObject(IloAny). A model is also created to manage the dimensions used by all models.

The solution process is iterative. Each depot model is improved and then the whole problem is improved. This latter phase is one that can cause visits to migrate from one depot to another. In other words, moves can be performed that cause a vehicle from a different depot to perform a visit. When the next iteration to improve depots begins, a synchronization needs to be performed. During this synchronization, the submodels are updated with the changes made during the improvement stage of the whole problem.

This problem demonstrates three main techniques of Dispatcher problem solving: the decomposition of a problem, a mixed iterative solving technique, and the maintenance of the coherence of submodels.

The first step is to write a natural language description of the problem.

The components of the routing model for this problem are the same as for a standard PDP, except that there are multiple depots. Vehicles are associated with a specific depot.

The constraints in this problem are the same as those in a standard PDP: vehicle capacity, time windows, and visit quantities.

The objective is to minimize the total cost of the solution, which is directly proportional to the total distance traveled by all vehicles.