In the vehicle routing problems presented in the previous lessons the goal was to perform visits located at given nodes. There is another type of problem where the goal is to visit arcs instead, arcs being a link between two nodes (arcs typically represent streets or road segments). This type of problem can involve activities such as winter gritting (dispensing salt or grit on snow-covered roads), door-to-door mail delivery, street cleaning, or garbage collecting. This chapter focuses on a particular type of problem called a Capacitated Arc Routing Problem (CARP) in which vehicles have a limited capacity.

The main difference in considering an arc problem is that a visit is not defined as a trip to a node, but is rather the path (arc) between two nodes. A quantity of a good is delivered to each arc and vehicles can carry a limited amount of goods (capacity). Time windows are not considered here although they could easily be modeled. All vehicles are identical and perform a single tour leaving and arriving at a unique depot.

Distances between nodes are computed from a graph representing the network of roads. For a given dimension d, the distance between two nodes n1 and n2 using a vehicle v is the sum of the value according to d of all the arcs on the cheapest path going from n1 to n2 using v. The cheapest path is the path of minimum cost using v. Furthermore, the distance between two visits located at arc (n1, n2) and arc (n3, n4) is defined to be the distance between nodes n2 and n3.

In this example, two extrinsic dimensions are used, one representing time and the other length. Both dimensions have their distance function based on the graph; the shortest path between two nodes depends on the arcs that are available in the graph. The cost function is a linear combination of the duration and of the length of the route of the vehicles.

The following figure shows a sample road network for an arc problem with eight nodes and 12 arcs (the example in this lesson has 52 nodes).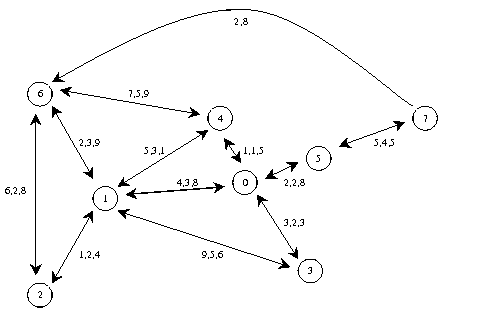

The arrows show in which direction an arc can be taken (a double arrow means it can be taken in both directions). The values on the arcs indicate respectively the duration in time and length of the arc. The third number represents the quantity of goods to be delivered to this arc; when a third number is not present the arc does not need to be visited.

The first step is to write a natural language description of the problem. A good way to start this process is to analyze the constraints and objectives. The primary constraint in this problem is that vehicles must deliver a quantity of goods to selected arcs on the road network. Not all arcs need to be visited (that is, have goods delivered along the arc), but those arcs may be travelled through anyway in order to minimize the travel cost.

The objective is to minimize the cost of the delivery of the quantity of goods along the arcs.