When the diameter increases from 2x to (2x+ß), with ß(>0) small at will, the number of optimal
nodes suddently grows since the optimal value increases from x to (x+1).
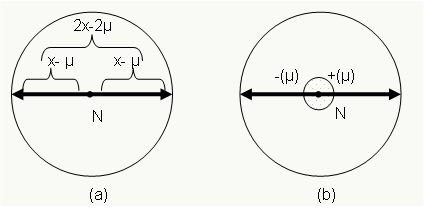
Figure 1
Optimal nodes are placed in general within a circle around the center of the network. Let us suppose
the presence of a node, say N, placed exactly in the center of the MANET.
Its value is x. Since N distance is (x-ε) from dense MANET boundary, with ε>=0,
only nodes placed within a distance of ε from N will value x.
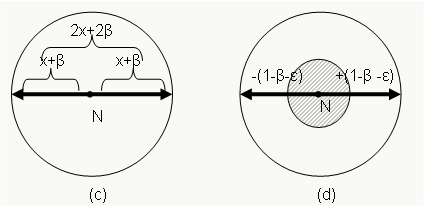
Figure 2
Now suppose that node N (placed in the center of the network) is (x+ß)
distant from the dense MANET boundary, with ß>0.
This suddently changes its value from x to (x+1). All nodes (x+1-ε), with ε>0,
far from most distant network nodes will weigh (x+1). Consequently, they all will be optimal.
These nodes are placed in a circle of radius (1-ß-ε) around N.
In conclusion, when the dense MANET diameter changes from 2x to (2x+ß), the number of optimal nodes greatly increases.


