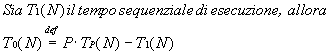
Solitamente si assume di avere mappato il problema nel modo migliore. Spesso però non si possono fare allocazioni così facili, in quanto sussistono problemi dinamici nella comunicazione dopo la allocazione.
A volte si usa la Funzione di Overhead Totale T0, cioè si tiene conto delle risorse e del tempo speso in comunicazione:
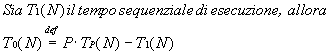
Osservazione: se si lavora con efficienza massima, l’overhead è nullo, quindi:
![]()
| Il tempo parallelo di esecuzione vale: |
|
| Lo speed-up vale: |
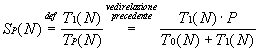 |
| L’efficienza quindi vale: |
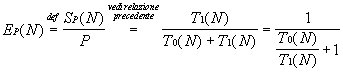 |
Applicando queste considerazioni al caso della somma di N numeri con P processori (problema dell’albero), considerando unitario il costo della somma e della comunicazione (H, uguale a lg P-1), risulta:
![]()
| L’overhead vale: |
|
| Lo speed-up vale: |
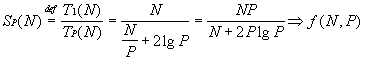 |
| L’efficienza quindi vale: |
|
Se calcoliamo ora L’Heavily Loaded Limit per il caso della somma di N numeri con P processori (problema dell’albero), considerando unitario il costo della somma e della comunicazione (H), risulta:
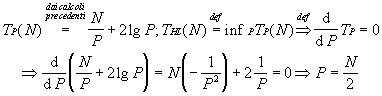
Il valore può non portare alla migliore efficienza. Per ottenere un’efficienza fissata al crescere di P bisogna calcolare il valore tale per cui si ottenga il migliore uso delle risorse.