47) Come vengono trattati i vari casi di complessità in un problema di dimensione N (somma di N interi) con P processori?

Sia

la complessità del sequenziale.

Complessità del parallelo nel caso identity size (N=P, quindi il fattore di carico è uguale ad 1).

Per sommare gli N interi si considerino i processori disposti come foglie di un albero binario. I valori fluiscono dalle foglie in su ed ogni nodo li somma ad ogni passo. Per le proprietà degli alberi binari vale:

, dove H è il percorso dalla radice alla foglia più lontana.

, cioè il numero di passi necessari è dell’ordine di grandezza del logaritmo del numero di processori, ovvero del numero di interi

, cioè la complessità in tempo del parallelo nel caso di P processori è uguale alla complessità del sequenziale di H, in quanto indipendentemente dal valore di P occorrono in ogni caso H passi sequenziali (ciò deriva solo dalle proprietà degli alberi binari e non da un particolare calcolo)

Lo speed-up vale:

L'efficenza vale:

quindi l’efficienza tende a zero al crescere del numero di processori.

Complessità del parallelo nel caso independent size.

Il lavoro viene suddiviso parallelizzandolo con un certo fattore di carico L. Si prevede una fase locale di lavoro ed una fase di scambio di informazioni per combinare i risultati parziali.

Vale:

Lo speed-up vale:

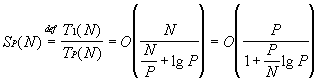L’efficienza vale:

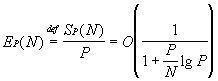Quindi: