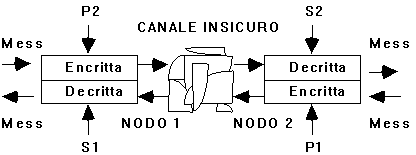
9) Cosa sono i sistemi a chiave pubblica?
Sono sistemi con l’encrittazione separata dalla decrittazione, con chiavi di decrittazione diverse
chiave pubblica o diretta: P (Kdiretta Kd)
chiave segreta o privata: S (Kinversa Ki)
L’invertibilità non è facile: con chiave pubblica e algoritmo non si riesce analiticamente a ricavare la chiave privata.

Si utilizzano funzioni unidirezionali: funzioni facilmente computabili ma la cui inversa non può essere computata a meno di informazioni sulla sua costruzione
L’algoritmo RSA è basato sul fatto che è molto difficile trovare i fattori di numeri molto grandi
si scelgano due numeri primi molto alti p e q (>10100)
siano: N=p*q e Z= (p-1)*(q-1)
come d (chiave di decrittazione) si scelga un numero primo rispetto a Z
per trovare e (chiave di encrittazione) si risolva l’equazione: e * d= 1 (mod Z)
quindi e*d è il più piccolo elemento nella serie Z+1, 2Z+1, 3Z+1 che è divisibile per d
Il messaggio viene preso a blocchi di f bit, con 2 alla f< N (in pratica f va da 256 a 512)
la funzione per encrittare il messaggio M è quindi: E’(e,N,M)=M alla e mod N
la funzione per decrittare il messaggio C è invece: D’(d,N,C)=C alla d mod N
Le funzioni E’ e D’ sono mutuamente inverse
La coppia <e,N> può essere considerata come una chiave di encrittazione Ke e come tale può essere distribuita
La coppia <d,N> può essere considerata come una chiave di decrittazione Kd e non può essere ricavata a partire da e e da N, salvo fattorizzare N per trovare p e q, ma poiché N>10200 il tempo di calcolo richiesto è enormemente grande ed il sistema è accettato.
Naturalmente il gestore deve conoscere entrambe le chiavi.
Problemi dei sistemi a chiave pubblica: